Medidas de posición
Cuartiles
Dada una muestra x1,x2,...,xn, podemos ordenar los datos de menor a mayor y dividirlos en cuatro partes con la misma cantidad de datos. Los cortes de estas divisiones son lo que llamamos cuartiles.
Cuando dividimos algo en dos partes, hacemos un corte; cuando dividimos en tres partes, hacemos dos cortes. Es decir, que para dividir nuestra data en cuatro partes, necesitamos tres cuartiles, identificados como Q1, Q2 y Q3.
Junto con el mínimo y el máximo, estos 5 valores sirven para resumir la distribución de una variable, con menos detalle que un histograma pero con más información que usando sólo la media y la varianza.
En python podemos usar el método describe para calcular estadísticas descriptivas básicas de un DataFrame. Estas incluyen
count: número de datos completosmean: Mediastd: Desviación típica25%: Q150%: Q275%: Q3max: Máximo
Vamos a descargar iris desde un repositorio público de github. Ya los nombres vienen en un formato legible y que cumple con las características del PEP8
import pandas as pd
iris = pd.read_csv("https://raw.githubusercontent.com/toneloy/data/master/iris.csv")
iris.head()## sepal_length sepal_width petal_length petal_width species
## 0 5.1 3.5 1.4 0.2 setosa
## 1 4.9 3.0 1.4 0.2 setosa
## 2 4.7 3.2 1.3 0.2 setosa
## 3 4.6 3.1 1.5 0.2 setosa
## 4 5.0 3.6 1.4 0.2 setosaAhora sí, calculemos el resumen de iris. Por defecto, .describe() toma en cuenta sólo columnas numéricas, así que en este resumen no tendremos información acerca de species.
iris.describe()## sepal_length sepal_width petal_length petal_width
## count 150.000000 150.000000 150.000000 150.000000
## mean 5.843333 3.057333 3.758000 1.199333
## std 0.828066 0.435866 1.765298 0.762238
## min 4.300000 2.000000 1.000000 0.100000
## 25% 5.100000 2.800000 1.600000 0.300000
## 50% 5.800000 3.000000 4.350000 1.300000
## 75% 6.400000 3.300000 5.100000 1.800000
## max 7.900000 4.400000 6.900000 2.500000Dos detalles interesantes:
- En inglés, Cuartil es Quartile. Por eso dice 1st Qu. y 3rd Qu.
- El segundo cuartil es igual a la Mediana, un estadístico que también se puede considerar una medida de tendencia central. En algunos libros también la podrías encontrar como un promedio no matemático
Pregunta
summary?
Rango intercuartílico
La diferencia entre el Q3 y Q1 es lo que llamamos Rango intercuartílico y lo representamos con IQR por Inter-quartile range. Es una medida de dispersión de los datos, ya que representa el ancho del 50% central de los datos. Mientras más dispersos estén los datos, mayor será esta distancia.
IQR=Q3−Q1
Representación gráfica
La manera más común de graficar los cuartiles es con un diagrama de cajas. También conocido como diagrama de caja y bigotes o por su nombre en inglés boxplot. En ggplot2 utilizamos la función geom_boxplot.
from plotnine import *
(ggplot(iris) +
geom_boxplot(aes(x=0, y="sepal_length")) +
labs(x="") +
theme(
axis_text_x=element_blank(),
axis_ticks_minor_x=element_blank(),
axis_ticks_major_x=element_blank()
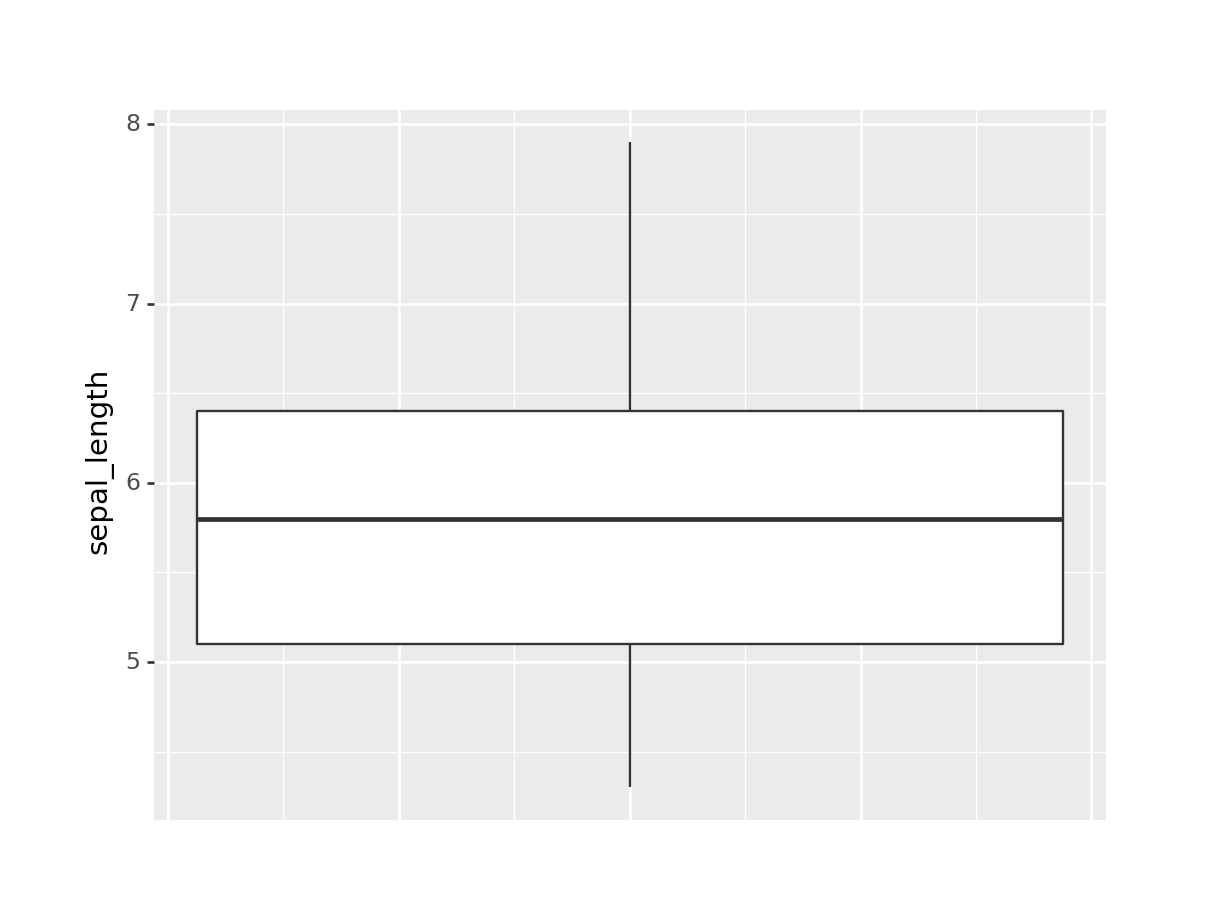
))## <ggplot: (298019932)>
En este gráfico, el eje x no significa nada, por eso eliminamos el texto y las marcas con la función theme. Después explicaremos más acerca de estas opciones de plotnine.
Pregunta
- Principal
- Central
- Significativo
- Representativo
Interpretación:
- La variable está representada en el eje y
- La línea horizontal del medio de la caja, la más gruesa, es la mediana
- La línea horizontal inferior de la caja es el 1er cuartil, y la línea horizontal superior es el 3er cuartil
- La altura de la caja es el Rango intercuartílico. Por lo tanto, mientras mayor sea la dispersión, más grande será la caja
- Cuando no hay valores atípicos, los extremos de las líneas verticales, llamados Bigotes son el mínimo y el máximo. Cuando hay valores atípicos, son los valores más bajos y altos que no sean valores atípicos.
- Los valores atípicos se definen en este contexto como valores más altos que Q3+(1.5∗IQR) o más bajos que Q1−(1.5∗IQR). Estos valores se representan con puntos.
Usar diagramas de caja para comparar
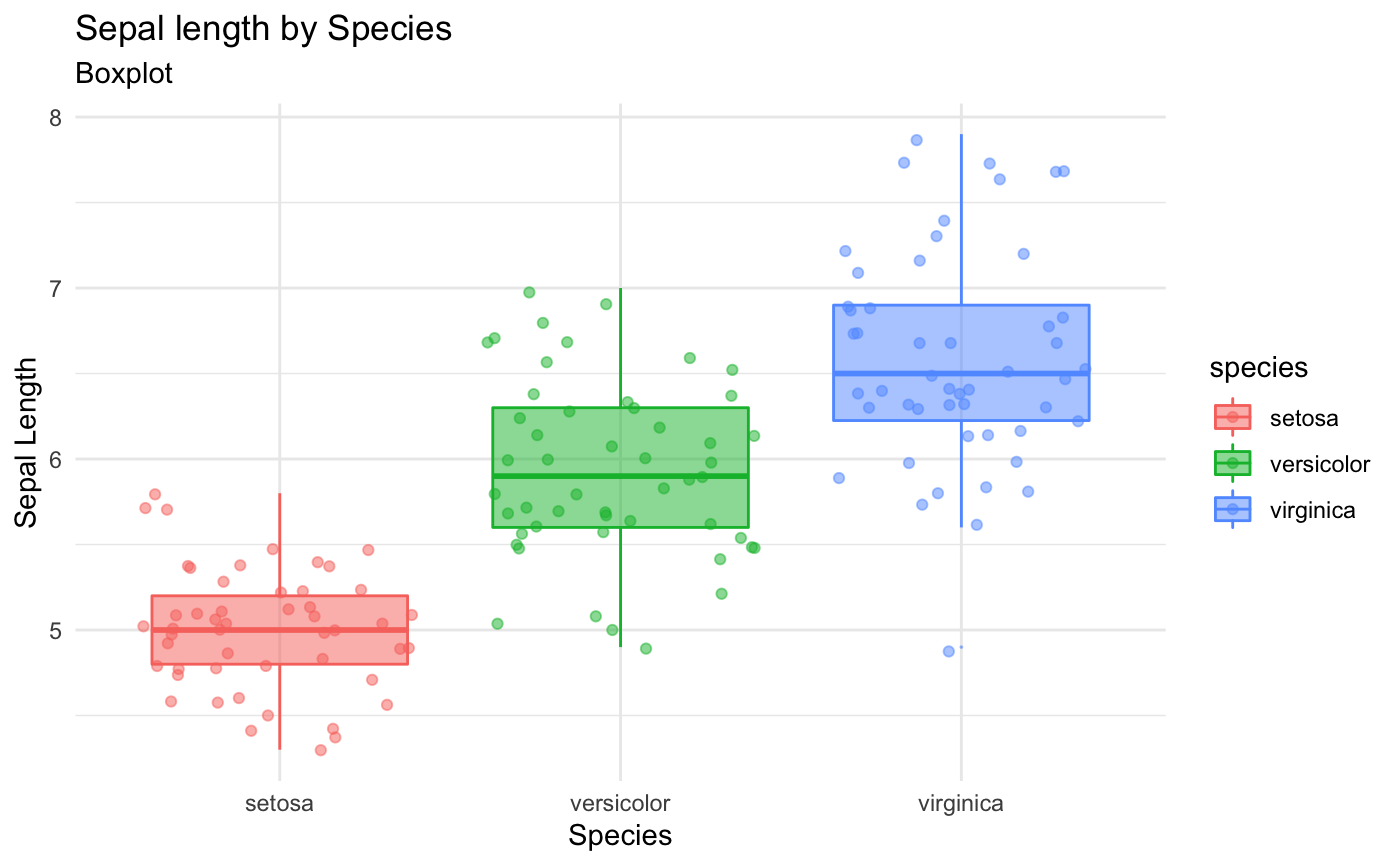
Una de las aplicaciones más útiles de los digramas de caja es comparar visualmente una variable en distintas categorías. Por ejemplo, si queremos comparar sepal_length pra las distintas species, graficaríamos las species en el eje de las x y sepal_length en el eje de las y
from plotnine import *
(ggplot(iris) +
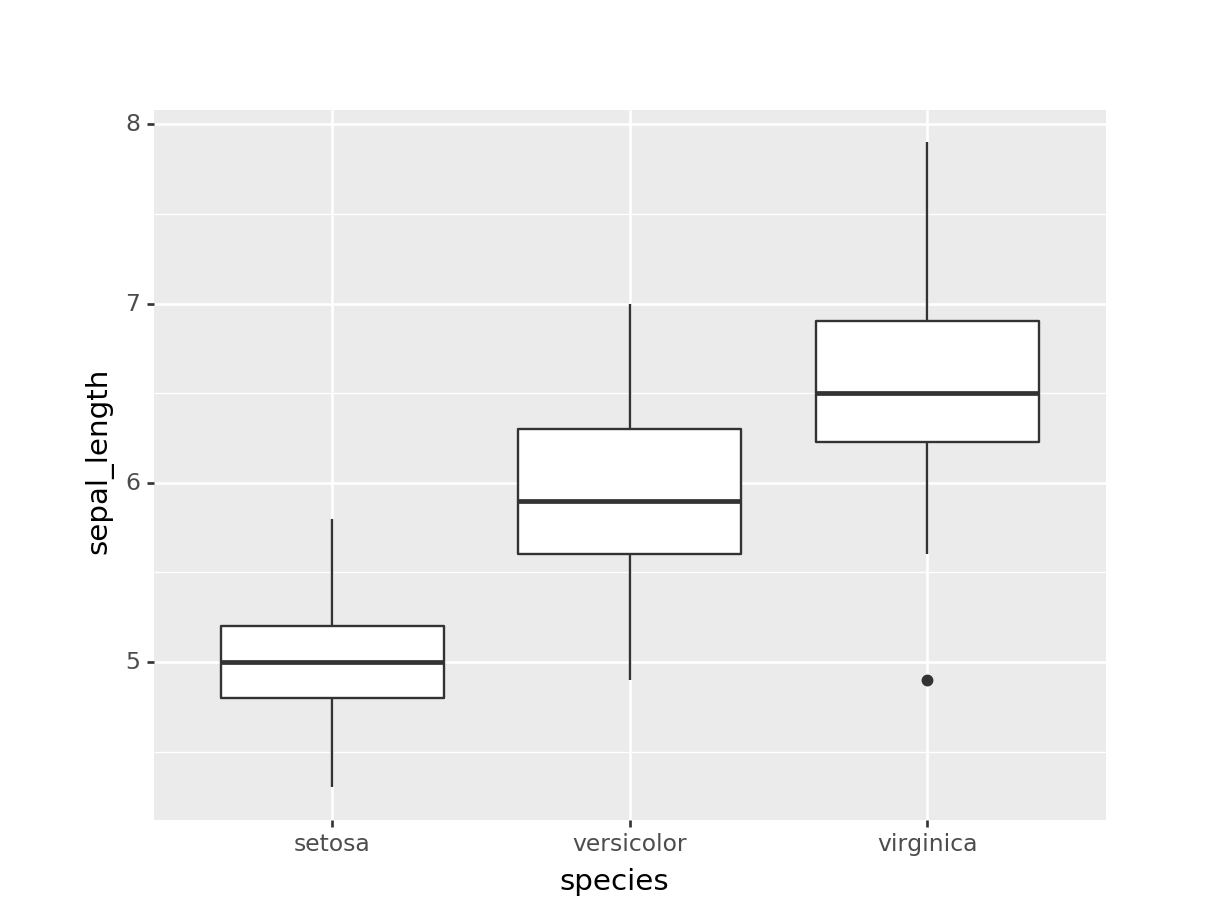
geom_boxplot(aes(x="species", y="sepal_length")))## <ggplot: (-9223372036553314118)>De un sólo vistazo nos damos cuenta que en general, los valores de sepal_length son mas bajos para setosa que para versicolor y virginica. Además, en el diagrama de caja de virginica podemos ver un punto atípico.
Por toda esta información que nos dan los digramas de caja tan rápidamente es que son los gráficos favoritos de los estadísticos; el problema es que más nadie los entiende ¡Tenemos tarea!
Deciles, Percentiles y Cuantiles (sí, con n en vez de r)
Podríamos dividir los datos en la cantidad de partes que queramos. Sin embargo, tradicionalmente se dividen los datos en 10 partes y en 100 partes, siendo las divisiones los Deciles y los Percentiles, respectivamente.
Otra forma de ver los cuartiles es que son los valores que dejan por debajo de estos el 25% (Q1), el 50% (Q2) y el 75% (Q3) de las observaciones en la muestra por debajo. Tiene sentido entonces pensar en obtener un estadístico que deje un porcentaje cualquiera de los valores por debajo. A este estadístico le llamamos Cuantil.
El método .quantile() devuelve por defecto la mediana
iris["sepal_length"].quantile()## 5.8O también podemos obtener un cuantil particular especificando un valor entre 0 y 1, donde 1 es equivalente al 100%.
iris["sepal_length"].quantile([.10, .25, .50, .75, .90])## 0.10 4.8
## 0.25 5.1
## 0.50 5.8
## 0.75 6.4
## 0.90 6.9
## Name: sepal_length, dtype: float64Pregunta
Pregunta
Conclusión y reflexiones
Las medidas de posición nos permiten resumir la distribución de una variable muy rápidamente, y si además utilizamos un diagrama de cajas, mejor. Esto las convierte en unas de las herramientas más poderosas de la estadística descriptiva.
Sin embargo, los que entendemos esto tenemos la tarea de explicarle a la mayor cantidad de gente. Estamos hablando de contenido de un curso introductorio de estadística, y muy poca gente sabría interpretar un diagrama de cajas, incluso en posiciones gerenciales o hasta autoridades públicas. En mi opinión personal, si queremos mejores decisiones en nuestras empresas y en nuestros países, la estadística debería parte de la cultura popular, y nuestros líderes deberían poder entender más allá de un gráfico de barras.
¡Tenemos tarea!