Tablas de frecuencia
La forma más simple de hacer estadística es contar. Una tabla de frecuencias es una manera fancy de decir tabla de conteo por categorías.
Veamos a ver cómo se construyen tablas de frecuencia en python utilizando pandas. ¡Listos para utilizar esto en el trabajo!
Vamos a descargar iris desde un repositorio público de github. Ya los nombres vienen en un formato legible y que cumple con las características del PEP8
import pandas as pd
iris = pd.read_csv("https://raw.githubusercontent.com/toneloy/data/master/iris.csv")
iris.head()## sepal_length sepal_width petal_length petal_width species
## 0 5.1 3.5 1.4 0.2 setosa
## 1 4.9 3.0 1.4 0.2 setosa
## 2 4.7 3.2 1.3 0.2 setosa
## 3 4.6 3.1 1.5 0.2 setosa
## 4 5.0 3.6 1.4 0.2 setosaTablas de frecuencia para variables cualitativas
Ahora sí, vamos a contruir la tabla de frecuencias para species.
(iris
.groupby("species")
.agg(frequency=("species", "count")))## frequency
## species
## setosa 50
## versicolor 50
## virginica 50
Esta sintaxis es la que personalmente más me gusta. Primero el método groupby agrupa por categoría. Luego lo interesante está en el método agg. Podemos pasar argumentos nombrados especificando la columna que queremos agregar y el método con el que la queremos agregar, en una tupla (“DataFrame resultante.
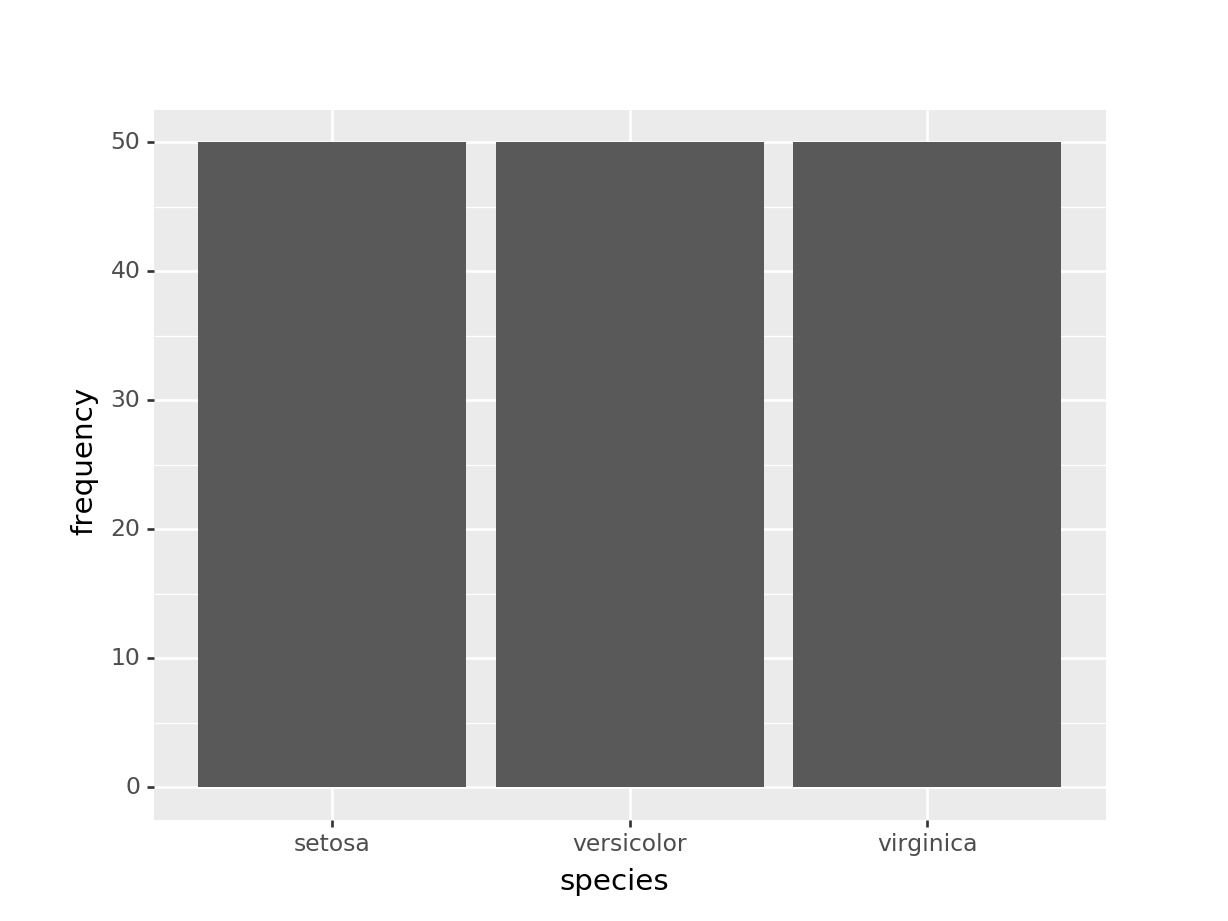
Según este resultado, las tres categorías de la variable species aparecen 50 veces cada una. Y ya está, ahí tienes una tabla de frecuencias.
Graficar una tabla de frecuencias
Lo más fácil para visualizar una tabla de frecuencias es utilizar un gráfico de barras. Vamos a utilizr la librería plotnine, un substituto de ggplot2 para python. Podríamos intentar trabajar con matplotlib, pero honestamente no me gusta para nada. Prefiero utilizar una librereia que utilice el Grammar of graphics y además, traducir de R a python va a ser más fácil.
from plotnine import *
freq_by_species = (iris
.groupby("species")
.agg(frequency=("species", "count"))
.reset_index())
(ggplot(freq_by_species, aes(x = "species", y = "frequency")) +
geom_bar(stat = 'identity'))## <ggplot: (297324601)>Pregunta
Si sumas todas las frecuencias ¿Qué resultado deberías tener?
- El tamaño de la muestra, n
- La suma de todos los valores de x
- No se puede saber
Pregunta
| Categoria | Frecuencia |
|---|---|
| Tipo 1 | 10 |
| Tipo 2 | 20 |
| Tipo 3 | X |
| Tipo 4 | 15 |
| n | 55 |
Tablas de frecuencia para variables cuantitativas
Supón que ahora quieres una tabla de frecuencias para sepal_length. Si sigues el mismo procedimiento, vas a terminar con un resultado prácticamente inútil.
(iris
.groupby("sepal_length")
.agg(frequency=("sepal_length", "count"))
.head())## frequency
## sepal_length
## 4.3 1
## 4.4 3
## 4.5 1
## 4.6 4
## 4.7 2Dos observaciones con respecto a este resultado:
- Hay 35 valores distintos para esta variable y leer una tabla tan larga no es práctico. Tuvimos que utilizar el método
head()para poder presentar algo razonable. - Puede ser más interesante agrupar valores cercanos, como 4.3 y 4.4; esta agrupación resuelve el punto 1 también.
Especificando el número de intervalos
Para agrupar valores de una variable cuantitativa en intervalos utilizamos la función pd.cut. El procedimiento entonces queda como:
iris["sepal_length_group"] = pd.cut(iris["sepal_length"], bins=5)
(iris
.groupby("sepal_length_group")
.agg(frequency=("sepal_length", "count")))## frequency
## sepal_length_group
## (4.296, 5.02] 32
## (5.02, 5.74] 41
## (5.74, 6.46] 42
## (6.46, 7.18] 24
## (7.18, 7.9] 11¡El resultado es que tenemos 5 categorías en una tabla más legible!
Especificando los cortes o límites de los intervalos
Aunque el resultado anterior no tiene nada incorrecto, podríamos hacer que los intervalos sean más legibles. El truco es que el argumento bins no sólo acepta el número de intervalos que queremos, sino que también podemos indicar los puntos en los que queremos hacer los cortes. Por ejemplo, vamos a hacer intervalos de longitud 1, desde el 4 hasta el 8. Esto lo podemos hacer con la función range.
list(range(4, 8+1, 1))## [4, 5, 6, 7, 8]También podríamos utilizar la función arange de numpy. Así podríamos hacer que la distancia entre los cortes sea un número con decimales, en vez de sólo enteros.
import numpy as np
np.arange(4, 8+0.5, 0.5)## array([4. , 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. ])
Tenemos que escribir 8+0.5 porque la función no incluye el último valor. De cierta manera, el rango es abierto a la derecha.
bins = list(range(4, 8+1, 1))
iris["sepal_length_group"] = pd.cut(iris["sepal_length"], bins=bins)
(iris
.groupby("sepal_length_group")
.agg(frequency=("sepal_length", "count")))## frequency
## sepal_length_group
## (4, 5] 32
## (5, 6] 57
## (6, 7] 49
## (7, 8] 12¡Mira qué linda tabla! A primera vista lo que se aprecia es que hay más valores bajos (entre 4 y 6) que altos (entre 6 y 8), y también que están más concentrados en el medio, (entre 5 y 6).
Los intervalos son abiertos a la izquierda y cerrados a la derecha. Esto implica que el 5 está incluído en el primer intervalo y no en el segundo
Frecuencias acumuladas
Podemos agregar una columna más a la tabla de frecuencias, acumulando las frecuencias para cada clase, utilizando la función cumsum.
bins = list(range(4, 8+1, 1))
iris["sepal_length_group"] = pd.cut(iris["sepal_length"], bins=bins)
sepal_length_counts = (iris
.groupby("sepal_length_group")
.agg(frequency=("sepal_length", "count")))
sepal_length_counts["cum_frequency"] = sepal_length_counts["frequency"].cumsum()
sepal_length_counts## frequency cum_frequency
## sepal_length_group
## (4, 5] 32 32
## (5, 6] 57 89
## (6, 7] 49 138
## (7, 8] 12 150Pregunta
| Categoria | Frecuencia | Frecuencia acumulada |
|---|---|---|
| (0 - 10] | - | 20 |
| (10 - 20] | - | 50 |
| (X - 30] | - | 80 |
| (30 - 40] | - | 100 |
- ¿Cuál es el tamaño de la muestra?
- ¿Cuál es la frecuencia del intervalo (10 - 20]?
- ¿Cuánto vale X?
Graficar una tabla de frecuencias de una variable cuantitativa
Podríamos seguir los mismo pasos que para una variable cualitativa y utilizar geom_bar
bins = list(range(4, 8+1, 1))
iris["sepal_length_group"] = pd.cut(iris["sepal_length"], bins=bins)
sepal_length_counts = (iris
.groupby("sepal_length_group")
.agg(frequency=("sepal_length", "count"))
.reset_index())
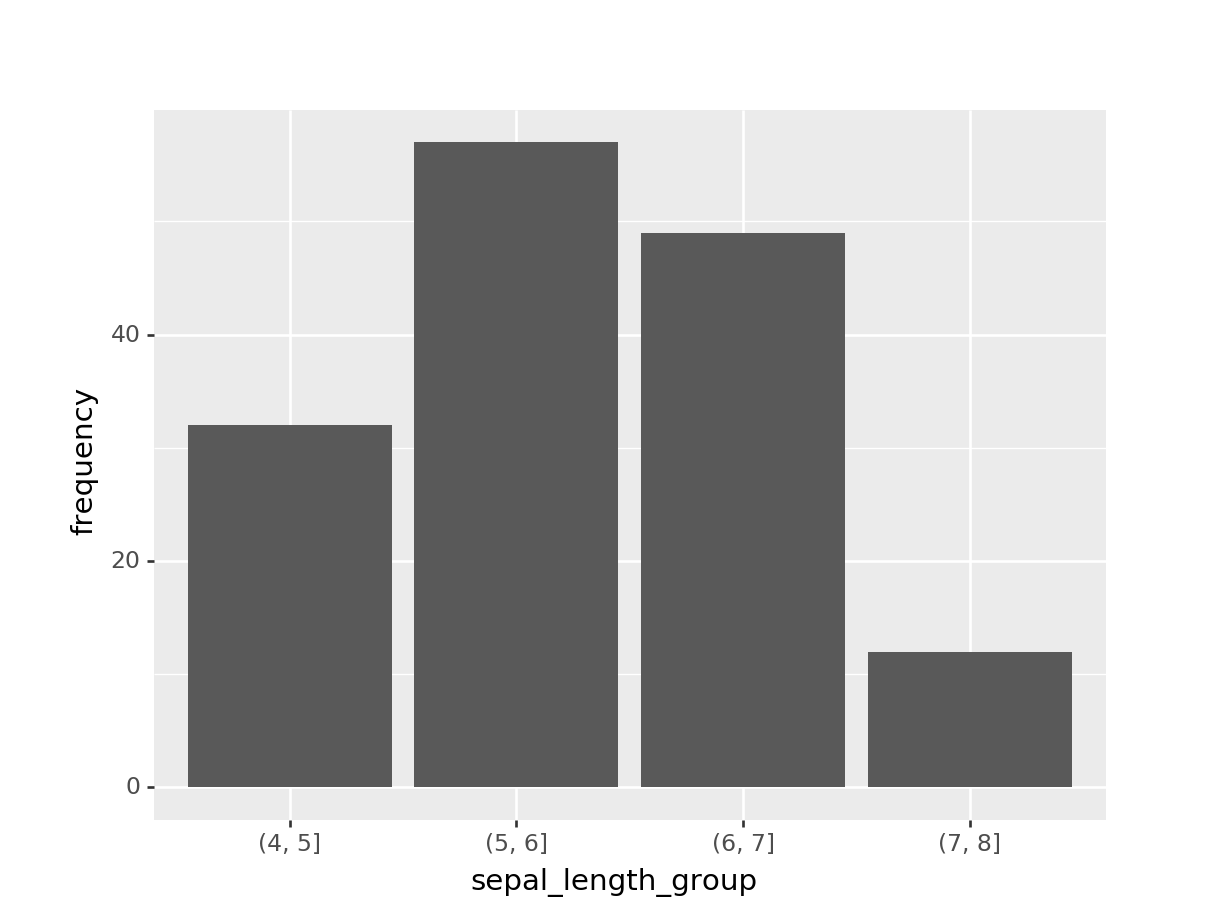
(ggplot(sepal_length_counts) +
geom_bar(aes(x = "sepal_length_group", y = "frequency"), stat = 'identity'))## <ggplot: (301623844)>Sin embargo, un histograma es más apropiado. Un histograma es un tipo particular de gráfico de barras. Las principales diferencias son:
- Las etiquetas en el eje de las x se colocan los límites de los intervalos
- Si hay algún intervalo cuya frecuencia sea 0, este intervalo sigue mostrándose en el eje x, mientras que en un gráfico de barras no necesariamente
- Como el límite superior de un intervalo es el límite inferior del siguiente, no hay espacio entre las barras
- Las barras podrían tener anchos distintos, aunque esto no es muy común
- En el eje de las y siempre van las frecuencias. Si no, no es un histograma
Como los histogramas son gráficos muy comunes, existe la función geom_histogram para ahorrarnos algunas líneas de código.
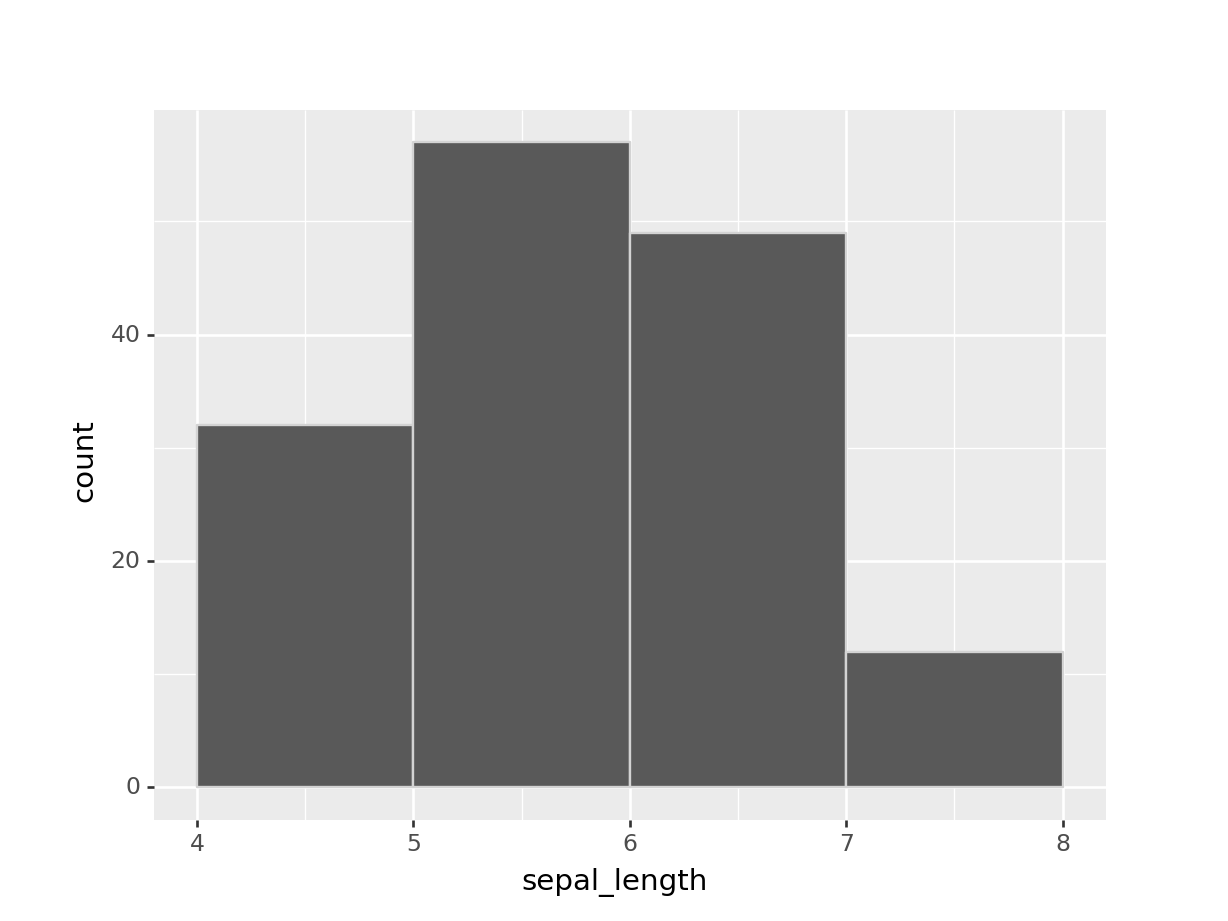
(ggplot(iris) +
geom_histogram(aes(x = "sepal_length"), binwidth=1, boundary=4, colour='lightgrey'))## <ggplot: (301635599)>Para tener el mismo gráfico que antes, especifiqué que el ancho de los intervalos sea bidwidth=1 y que uno de los límites sea boundary=4. También agregué colour='lightgrey' para que los bordes fuesen gris claro; no es necesario, pero me gusta más cómo se ve así que sin separación entre las barras.
Ya que estamos viendo todo en un gráfico y no hay que leer, nos podemos dar el lujo de tener intervalos más cortos y por lo tanto más intervalos y más detalle.
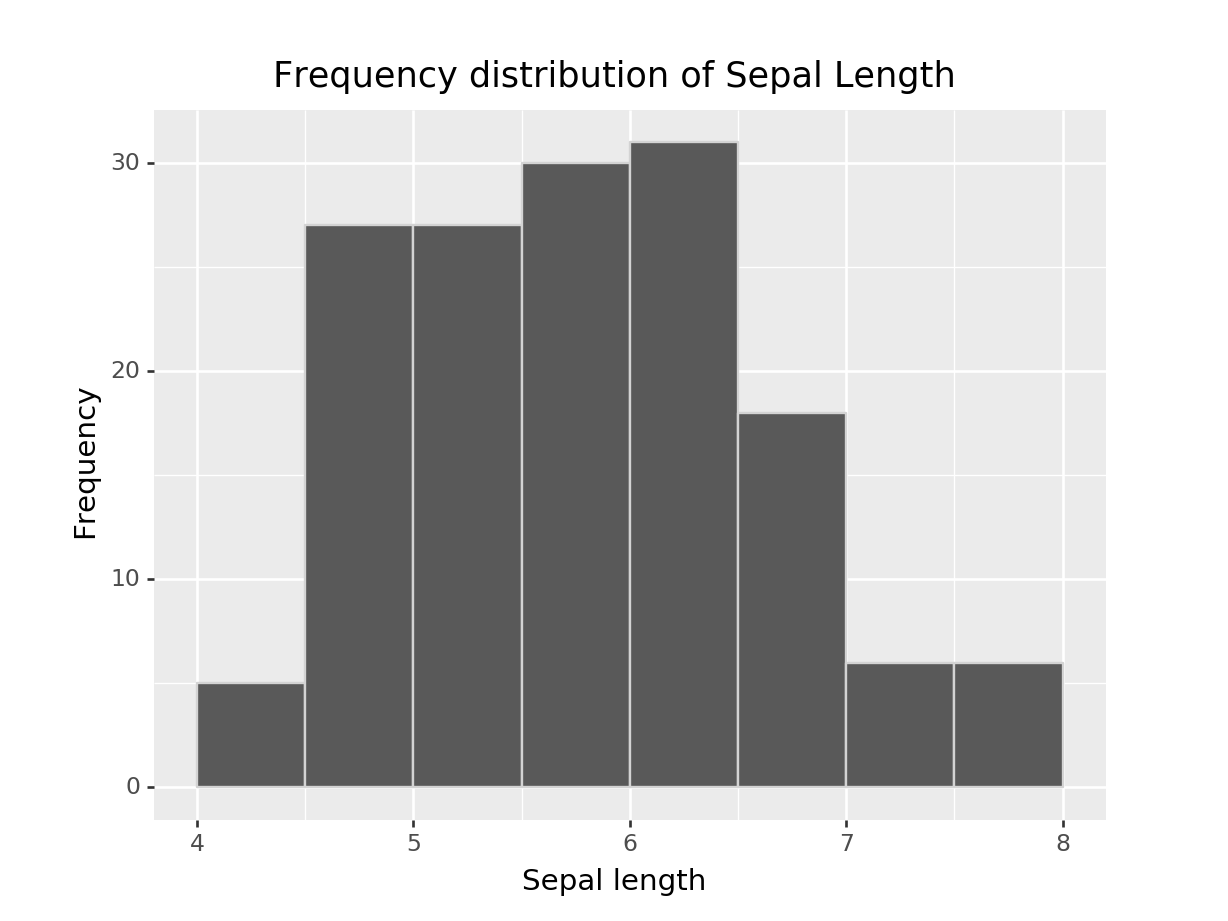
import numpy as np
breaks = np.arange(4, 8+0.5, 0.5)
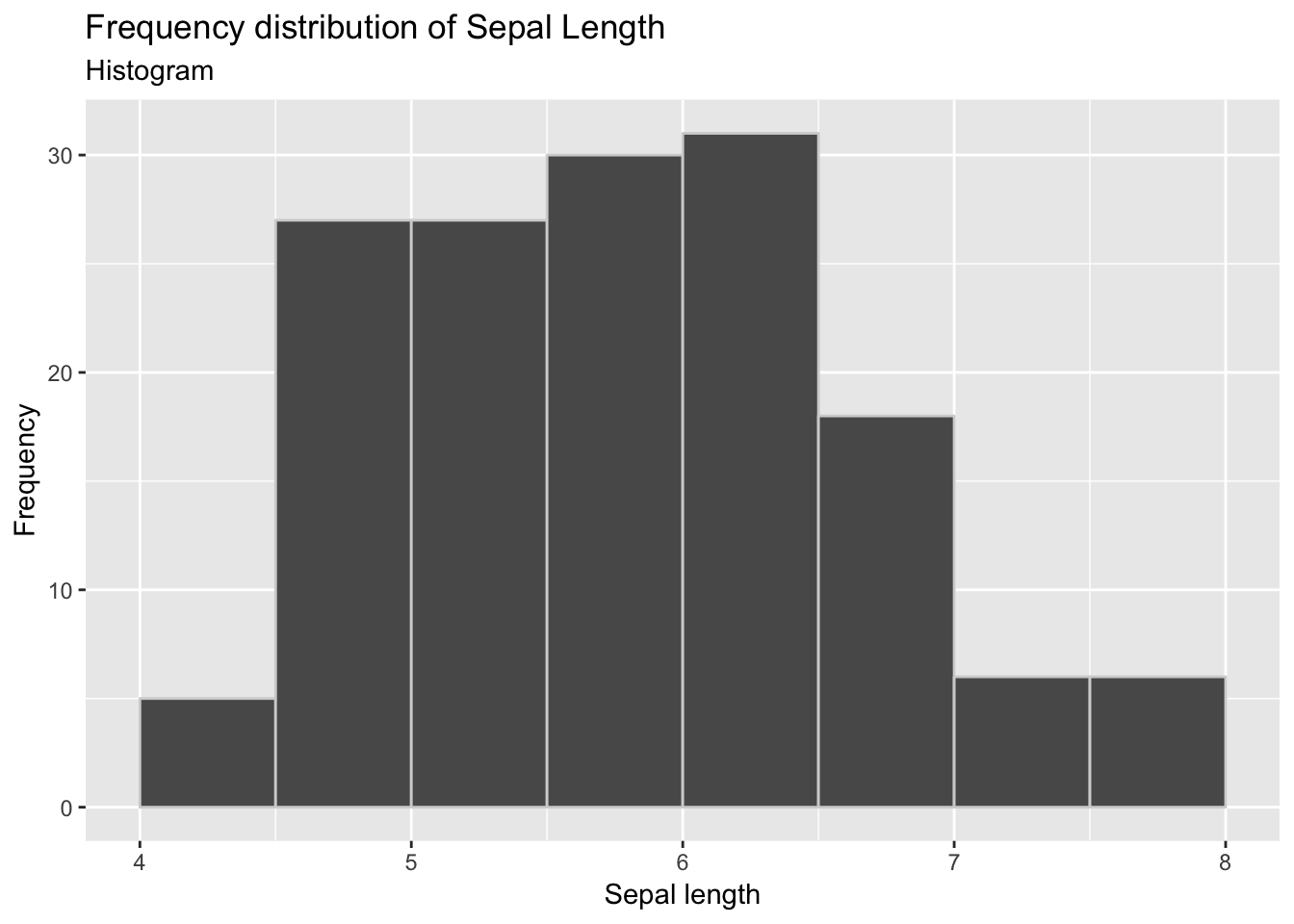
(ggplot(iris) +
geom_histogram(aes(x = "sepal_length"), breaks=breaks, colour='lightgrey') +
ggtitle('Frequency distribution of Sepal Length') +
labs(x='Sepal length', y='Frequency'))## <ggplot: (-9223372036552836548)>Conclusión
Las tablas de frecuencia son una herramienta bastante útil para saber de qué va una variable, y además se contruyen súper fácil en python. También vimos lo fácil que es visualizar las tablas con un gráfico de barras en el caso de una variable cualitativa y con un histograma en el caso de una variable cuantitativa. Además, con saber usar ggplot2 ya tenemos el 90% del trabajo para saber usar plotnine, una oferta 2x1 que no se puede desaprovechar.