Varianza y desviación típica
Introducción
La idea detrás de las medidas de dispersión es entender qué tan distintos son los valores entre sí. Intuitivamente sabemos que si todos los valores son iguales, la dispersión o diversidad de los datos es nula. Pero cuando los valores son distintos ¿cómo medir la diferencia entre estos?
Uno de los enfoques más comúnmente utilizados es tomar una medida de tendencia central como la media y comparar todos los valores con esta. Hay quienes opinan (incluyéndome) que no tiene sentido reportar una medida de tendencia central sin acompañarla de al menos una medida de dispersión apropiada. Pero primero necesitamos que más gente entienda lo que son las medidas de dispersión ¡Tenemos tarea!
… necesitamos que más gente entienda lo que son las medidas de dispersión ¡Tenemos tarea!
Vamos a descargar iris desde un repositorio público de github. Ya los nombres vienen en un formato legible y que cumple con las características del PEP8
import pandas as pd
iris = pd.read_csv("https://raw.githubusercontent.com/toneloy/data/master/iris.csv")
iris.head()## sepal_length sepal_width petal_length petal_width species
## 0 5.1 3.5 1.4 0.2 setosa
## 1 4.9 3.0 1.4 0.2 setosa
## 2 4.7 3.2 1.3 0.2 setosa
## 3 4.6 3.1 1.5 0.2 setosa
## 4 5.0 3.6 1.4 0.2 setosaPrimer intento: promediar los desvíos
Un enfoque intuitivo es promediar las diferencias de cada valor con la media:
∑ni=1(xi−ˉX)n
A la expresión (xi−ˉX) se le conoce como desvío. Es decir, podemos leer la fórmula como la suma de los desvíos dividida entre el tamaño de la muestra.
El problema con esto es que siempre es cero (y en la universidad lo vas a tener que demostrar… ¡SUSTO!).
iris["sepal_length_deviations"] = iris["sepal_length"] - iris["sepal_length"].mean()
iris["sepal_length_deviations"].mean()## -3.315866100213801e-16Desviación media
Tenemos que solucionar el problema del cero. Lo que sucede es que los desvíos positivos (cuando xi>ˉX) se cancelan con los desvíos negativos (cuando xi<ˉX). Una solución lógica es hacer que todos sean positivos y entonces promediamos. Esto lo logramos utilizando el valor absoluto de los desvíos. A esta medida la llamamos desviación media:
DM=∑ni=1|xi−ˉX|n
Con pandas podemos calcular esta desviación media con el método .mad():
md = iris["sepal_length"].mad()
md## 0.6875555555555557Es decir, en promedio los valores están a 0.688 unidades de la media.
Entonces ¿fin de la historia, no? Pues desafortunadamente, no. Aunque la desviación media tiene la ventaja de ser fácilmente interpretable, el valor absoluto es una función con una característica matemática que la hace complicada. Esta propiedad hace que sea difícil construir más métodos con base en la Desviación Media, y por esto su uso no es tan frecuente.
Para los curiosos, estudiosos o que sepan algo de cálculo diferencial, el problema del valor absoluto es que no es diferenciable en todo su dominio. Específicamente, no es diferenciable el cero.
Varianza
En vez de tomar el valor absoluto, podríamos elevar los desvíos al cuadrado. El resultado es lo que se conoce como Varianza y se representa con S2
S2=∑ni=1(xi−ˉX)2n
Con la varianza ganamos en propiedades matemáticas pero es menos interpretable ¿Por qué es más utilizada que la desviación media? En primer lugar, porque hay un montón de métodos estadísticos más avanzados que utilizan la suma de los desvíos al cuadrado, así que se prefiere utilizar siempre el mismo principio para medir la dispersión. En segundo lugar, pues simplemente por tradición o convención.
También por propiedades matemáticas, se prefiere cambiar el denominador por n−1 en lugar de n. A este estadístico se le conoce como Cuasi-varianza y se denota con ˆS2:
ˆS2=∑ni=1(xi−ˉX)2n−1
Nuevamente, para los curiosos y estudiantes cerebritos, la Cuasi-varianza es un estimador insesgado. Este concepto viene de lo que se conoce como estadística matemática o inferencia estadística. Se dice que un estimador es insesgado si su esperanza matemática es igual al parámetro que estima.
El símbolo ^ se lee circunflejo, techo o sombrero ¿Cuál es la manera correcta? Mi opinión es que cualquiera, siempre y cuando te entiendan, aunque circunflejo es probablemente la que más sentido tiene desde el punto de vista lingüístico.
Cálculo en python
En python podemos calcular la cuasi-varianza utilizando el método var. Esta función también omite los valores faltantes, como con la media.
iris["sepal_length"].var()## 0.6856935123042507Si queremos calcular la varianza, utilizamos el argumento ddof=0. El denominador en la fórmula será entonces n−ddof=0.
iris["sepal_length"].var(ddof=0)## 0.6811222222222223Propiedades de la varianza y la cuasi-varianza
Dada una muestra x1,x2,...,xn, se puede demostrar que la varianza, S2X cumple con las siguientes propiedades:
- Si a una variable la multiplicamos por una constante, tendremos que multiplicar la varianza (o la cuasi-varianza) por esta constante al cuadrado. Por otro lado, si le sumamos una constante, esto no afectará la varianza. Formalmente, si aplicamos la transformación lineal yi=axi+b y calculamos la varianza, obtendremos el resultado S2Y=a2SX.
iris["petal_length_plus_one"] = iris["petal_length"] + 1
iris["petal_length_double"] = iris["petal_length"] * 2
iris["petal_length"].var()## 3.116277852348993iris["petal_length_plus_one"].var()## 3.116277852348994iris["petal_length_double"].var()## 12.465111409395972- La menor suma de desvíos al cuadrado que podemos obtener es cuando la calculamos con respecto de la media. Formalmente:
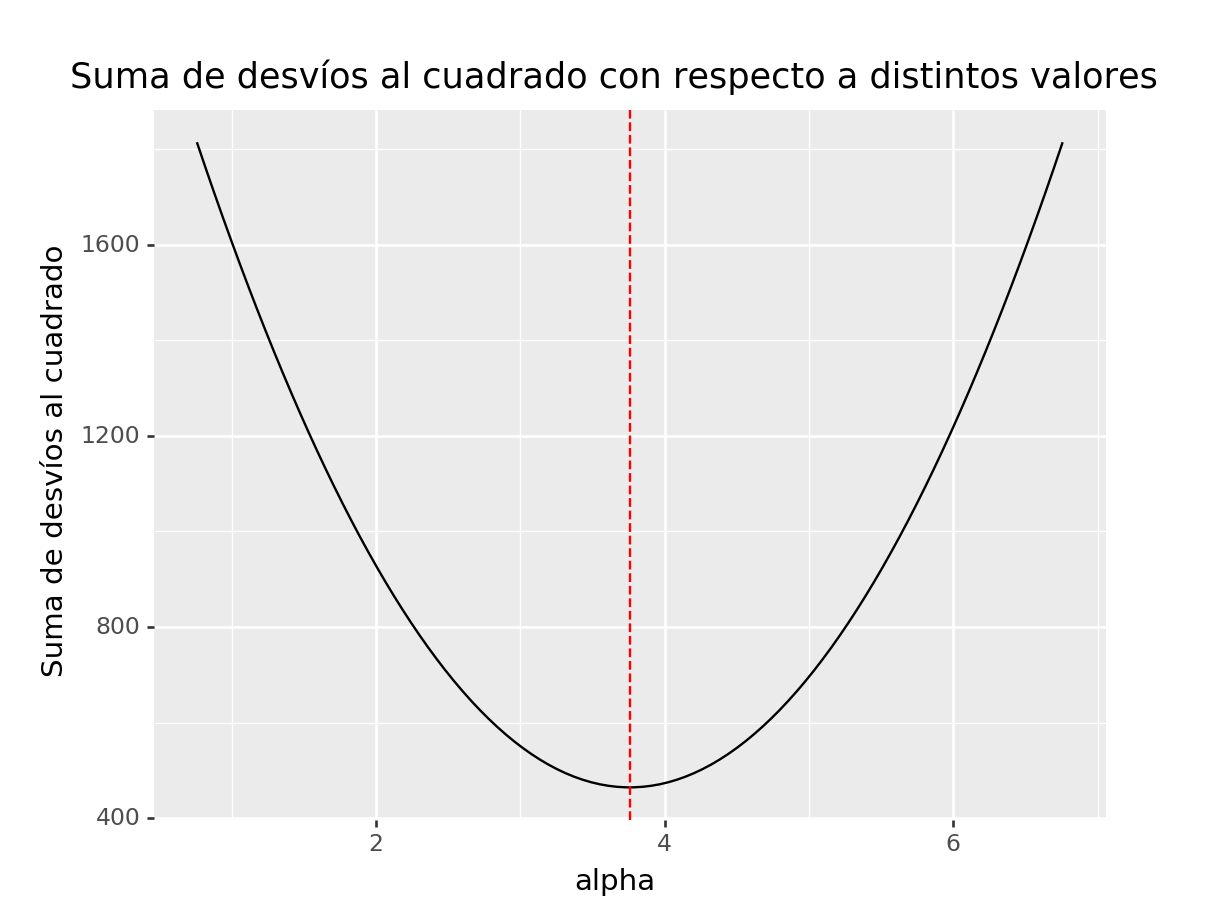
minαn∑i=1(xi−α)2=n∑i=1(xi−ˉX)2
Esto nos da un criterio objetivo para elegir cuál medida de tendencia central utilizamos para calcular la suma de desvíos al cuadrado. Vamos a graficar la suma de desvíos al cuadrado para distintos valores de α y comprobar gráficamente que esta suma es mínima si α=ˉX.
import numpy as np
from plotnine import *
mean_petal_length = iris["petal_length"].mean()
min_petal_length = mean_petal_length - 3
max_petal_length = mean_petal_length + 3
alpha_n_steps = 100
alpha_step = (max_petal_length - min_petal_length) / (alpha_n_steps + 1)
alpha_values = np.arange(min_petal_length, max_petal_length+alpha_step, alpha_step)
alpha_values = np.append(alpha_values, iris["petal_length"].mean())
def sum_of_squares(alpha, df, column):
square_deviations = (df[column] - alpha).pow(2)
df = pd.DataFrame({"ss": [square_deviations.sum()], "alpha": [alpha]})
return df
ss = pd.concat([sum_of_squares(alpha, iris, "petal_length") for alpha in alpha_values])
(ggplot(ss, aes(x="alpha", y="ss")) +
geom_line() +
geom_vline(aes(xintercept=mean_petal_length), linetype="dashed", colour="red") +
ggtitle("Suma de desvíos al cuadrado con respecto a distintos valores") +
labs(y="Suma de desvíos al cuadrado")
)## <ggplot: (302177358)>- La varianza de una constante es 0
constant = pd.Series([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
constant.var()## 0.0Pregunta
Desviación típica
La varianza y cuasi-varianza tienen el problema de estar expresadas en las mismas unidades de la variable original ¡pero al cuadrado! Por ejemplo, sepal_length está medida en centímetros, por lo tanto, la varianza que acabamos de calcular está en centímetros cuadrados. Una solución es sacar la raíz cuadrada. A estos nuevos estadísticos se les conoce como Desviación típica o Cuasi-desviación típica, según sea el caso.
Desviación típica
S=√S2
Cuasi-desviación típica
ˆS=√ˆS2
En python, utilizamos el método .std() para calcular la cuasi-desviación típica. Para calcular la desviación típica, nuevamente utilizamos ddof=0.
iris["sepal_length"].std()## 0.828066127977863iris["sepal_length"].std(ddof=0)## 0.8253012917851409En la literatura en castellano también se substituye típica por estandar. Este tema con los nombres es muy habitual en estadística y tiene que ver en parte con que mucha de la literatura es traducida de otros idiomas como inglés, francés, ruso, italiano, etc.
Propiedades de la desviación típica
Dada una muestra x1,x2,...,xn, se puede demostrar que la desviación típica, SX cumple con las siguientes propiedades:
Si a una variable la multiplicamos por una constante, tendremos que multiplicar la desviación típica (o la cuasi-desviación) por esta misma constante. Por otro lado, si le sumamos una constante, esto no afectará la desviación típica. Formalmente, si aplicamos la transformación lineal yi=axi+b y calculamos la varianza, obtendremos el resultado SY=aSX.
La desviación típica de una constante es 0
Pregunta
¿Cómo comprobarías estas propiedades en python? Para esta pregunta no te damos la respuesta. Simplemente comprueba que el resultado que te da python es lo que dicen las propiedades de la desviación.
¿Cómo se ve la dispersión?
Vamos a comparar la desviación típica de sepal_length para las distintas species:
(iris
.groupby("species")
.agg(sepal_length_sd=("sepal_length", "std")))## sepal_length_sd
## species
## setosa 0.352490
## versicolor 0.516171
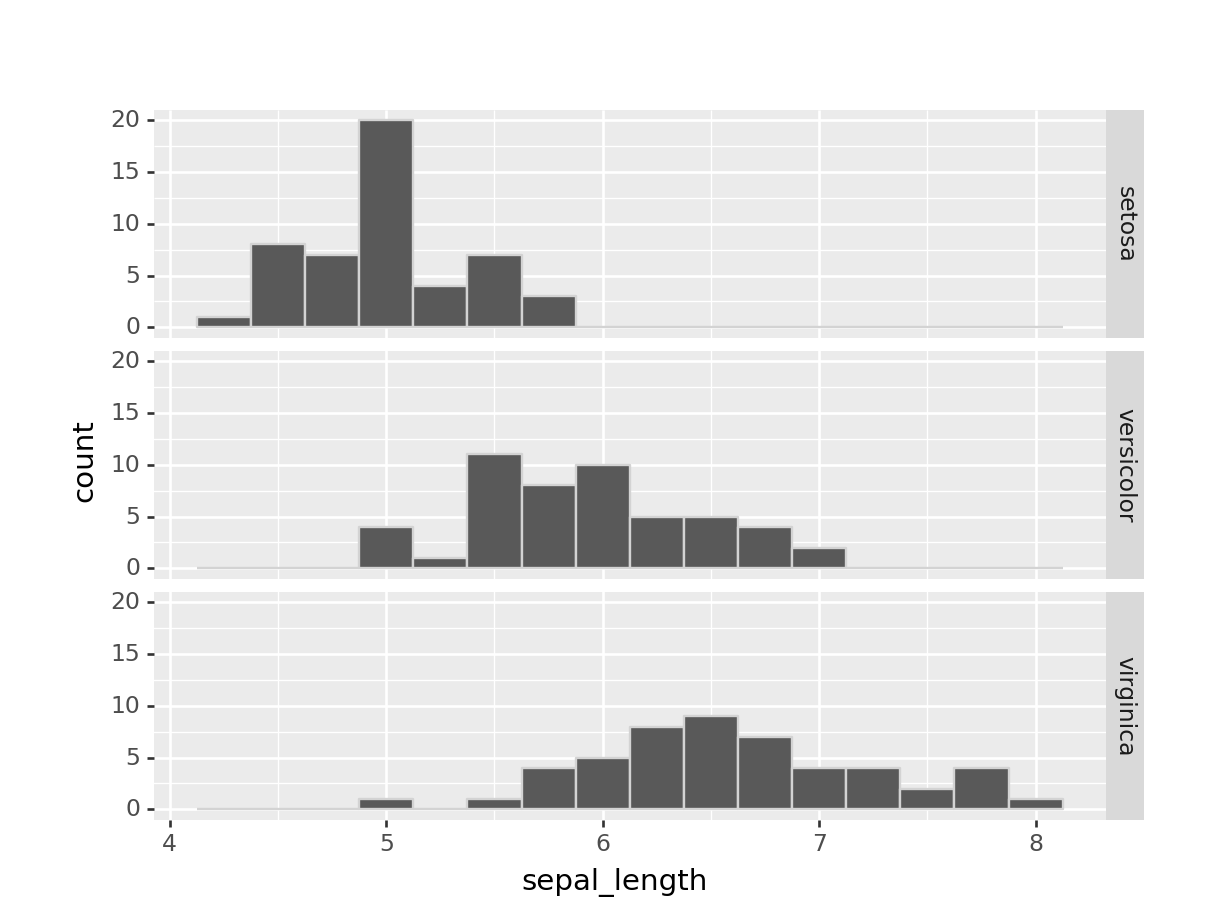
## virginica 0.635880Según este resultado, las flores setosa son más parecidas entre sí que las otras dos especies porque tienen una cuasi-desviación típica menor. Esto se puede apreciar al graficar el histograma para cada especie:
from plotnine import *
(ggplot(iris) +
geom_histogram(aes(x="sepal_length"), binwidth=0.25, colour='lightgrey') +
facet_grid("species ~ ."))## <ggplot: (-9223372036557458579)>Vemos cómo los valores de sepal_length de las setosa están más concentrados en el medio del histograma, mientras que en el otro extremo tenemos que para las virginica, los valores están más dispersos.
Conclusión
Las medidas de dispersión no son muy populares fuera de las clases de estadística por la complejidad de su interpretación, pero son necesarias al tratar de resumir las características de un conjunto de datos en unos pocos números. Por regla general, acompaña cualquier medida de tendencia central con una o más medidas de dispersión y con gráficos Hay otras medidas de dispersión que vale la pena explorar como el coeficiente de variación, el rango intercuartílico o el coeficiente de Gini, pero las dejaremos para otro post para no complicar este más de lo necesario.