Covarianza
La estadística no sólo sirve para entender cada variable por separado, sino que también podemos entender las relaciones entre dos o más variables, gráficamente y a través de estadísticos. En este caso vamos a hablar acerca de las relaciones entre dos variables cuantitativas utilizando la Covarianza y la Correlación.
Diagrama de dispersión
Dadas una muestra (x1,y1),(x2,y2),...,(xn,yn) en la que se miden las variables X e Y para cada elemento, podríamos graficar estos pares de puntos en un eje cartesiano.
Vamos a limpiar nuestros datos para luego hacer los cálculos en R.
library(dplyr)
library(janitor)
iris <- iris %>% as_tibble() %>% clean_names()Y ahora vamos a graficar el diagrama de dispersión entre petal_length y petal_width utilizando la función geom_point de ggplot2.
library(ggplot2)
iris %>%
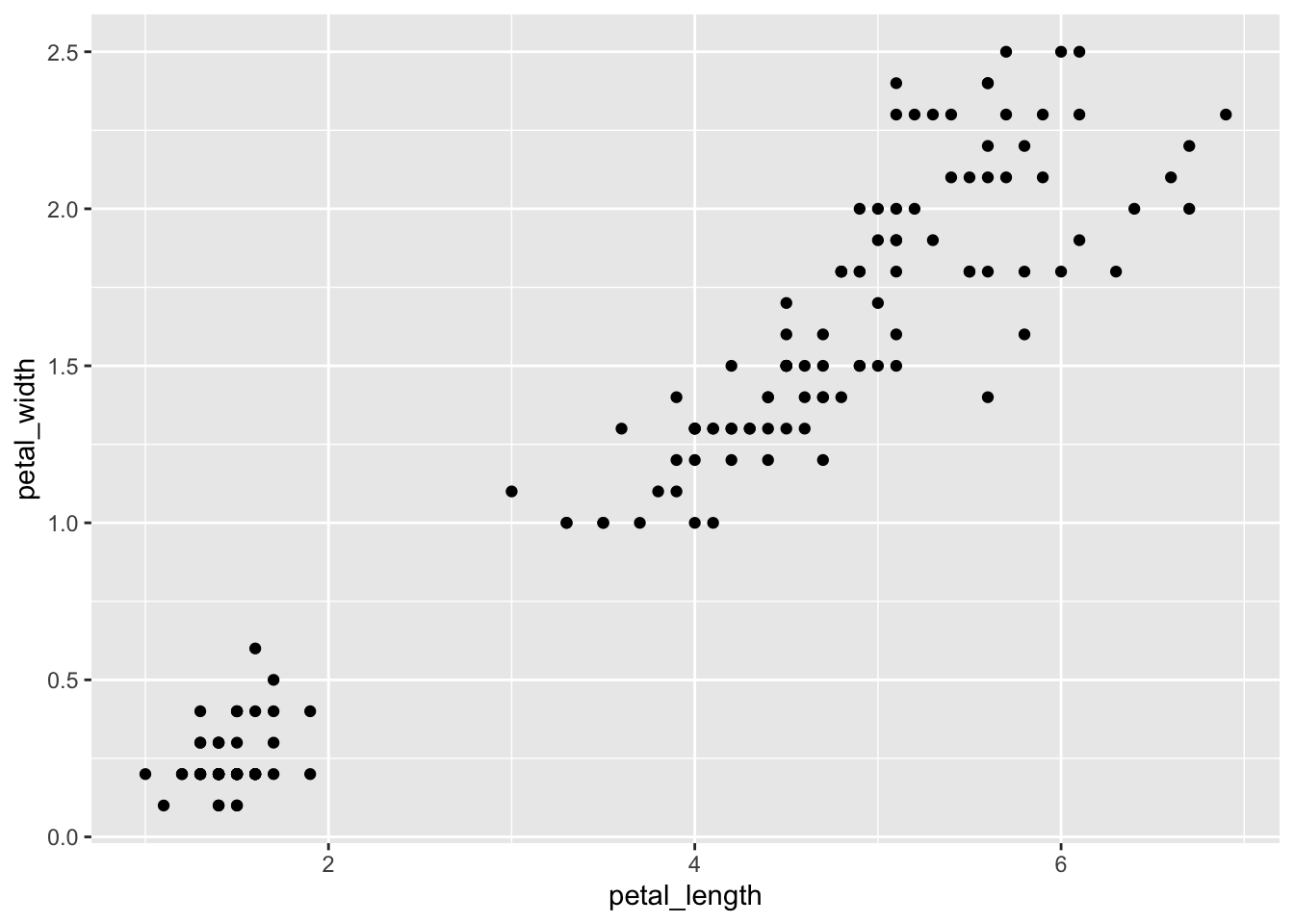
ggplot(aes(x = petal_length, y = petal_width)) +
geom_point()Por lo que podemos ver en el gráfico, pareciera que lo valores altos de petal_length van con valores altos de petal_width (y viceversa).
Covarianza
Si tenemos la misma muestra (x1,y1),(x2,y2),...,(xn,yn) podemos calcular la covarianza Covarianza como
SXY=∑ni=1(xi−ˉX)(yi−ˉY)n−1
Directamente utilizaremos el denominador n−1 para ser consistentes con la mayoría de la literatura y con el cálculo en R.
Con este estadístico medimos el signo de la relación lineal entre X e Y:
- Si SXY=0 entonces no existe relación lineal entre X e Y
- Si SXY>0 entonces existe una relación lineal directa o positiva entre X e Y. Esto es, a mayores valores de X, en promedio tenemos mayores valores de Y y viceversa.
- Si SXY<0 entonces existe una relación lineal inversa o negativa entre X e Y. Esto es, a mayores valores de X, en promedio tenemos menores valores de Y y viceversa.
Pregunta
- La relación lineal entre las variables es directa y fuerte
- La relación lineal entre las variables es fuerte
- La relación lineal entre las variables es directa
- La relación lineal entre las variables es inversa
- La relación lineal entre las variables es inversa y fuerte
Cálculo de la covarianza en R
En R, utilizamos la función cov para calcular la covarianza entre dos vectores o columnas de un data.frame.
library(tidyr)
iris %>%
summarise(
cov_petal_length__petal_width = cov(petal_length, petal_width),
cov_petal_length__sepal_width = cov(petal_length, sepal_width)
)## # A tibble: 1 x 2
## cov_petal_length__petal_width cov_petal_length__sepal_width
## <dbl> <dbl>
## 1 1.30 -0.330Pregunta
petal_length y sepal_width?
Propiedades de la covarianza
Dada una muestra (x1,y1),(x2,y2),...,(xn,yn), se cumplen las siguientes propiedades relacionadas con la covarianza SXY:
- Si transformamos linealmente las variables originales X′=a+bX, Y′=c+dY, la covarianza SX′Y′ entre X′, Y′ es la covarianza original multiplicada por bd. Las constantes que se suman no alteran el resultado. En fórmula, tenemos
SX′Y′=bdSXY
iris %>%
summarise(
cov_1 = cov(petal_length, petal_width),
cov_2 = cov(5 + 2 * petal_length, 3 - 4 * petal_width),
cov_3 = 2 * (-4) * cov(petal_length, petal_width)
)## # A tibble: 1 x 3
## cov_1 cov_2 cov_3
## <dbl> <dbl> <dbl>
## 1 1.30 -10.4 -10.4- La covarianza de una variable consigo misma es la varianza de la variable
SXX=S2X
iris %>%
summarise(
cov = cov(petal_length, petal_length),
var = var(petal_length)
)## # A tibble: 1 x 2
## cov var
## <dbl> <dbl>
## 1 3.12 3.12- La covarianza entre X e Y es igual a la covarianza entre Y y X
SXY=SYX
iris %>%
summarise(
cov_1 = cov(petal_length, petal_width),
cov_2 = cov(petal_width, petal_length),
)## # A tibble: 1 x 2
## cov_1 cov_2
## <dbl> <dbl>
## 1 1.30 1.30- La covarianza puede calcularse también de la siguiente manera
SXY=∑ni=1xiyin−1−nn−1ˉXˉY
cov_alt <- function(.x, .y) {
n <- length(.x)
(sum(.x * .y) / (n - 1)) - (n / (n - 1)) * mean(.x) * mean(.y)
}
iris %>%
summarise(
cov_1 = cov(petal_length, petal_width),
cov_2 = cov_alt(petal_length, petal_width),
)## # A tibble: 1 x 2
## cov_1 cov_2
## <dbl> <dbl>
## 1 1.30 1.30En ocasiones, esta formulación es más sencilla de calcular que la de la definición, incluso para las computadoras.
- Dada la variable Z=X+Y, podemos calcular la varianza de Z en función de las varianzas de X, Y y de su covarianza
S2Z=S2X+2SXY+S2Y
iris %>%
summarise(
var_1 = var(petal_length + petal_width),
var_2 = var(petal_length) + 2*cov(petal_length, petal_width) + var(petal_width),
)## # A tibble: 1 x 2
## var_1 var_2
## <dbl> <dbl>
## 1 6.29 6.29- Dada la variable Z=X−Y, podemos calcular la varianza de Z en función de las varianzas de X, Y y de su covarianza
S2Z=S2X−2SXY+S2Y
La diferencia de esta propiedad con la anterior es el signo del coeficiente de la covarianza. En ambos casos, las varianzas se suman.
Pregunta
- La covarianza de una variable X con una constante c es 0
iris %>%
mutate(
constant = 10
) %>%
summarise(
cov = cov(petal_length, constant),
)## # A tibble: 1 x 1
## cov
## <dbl>
## 1 0Pregunta
- 0
- 1
- No se puede saber
Cómo se ve la cóvarianza
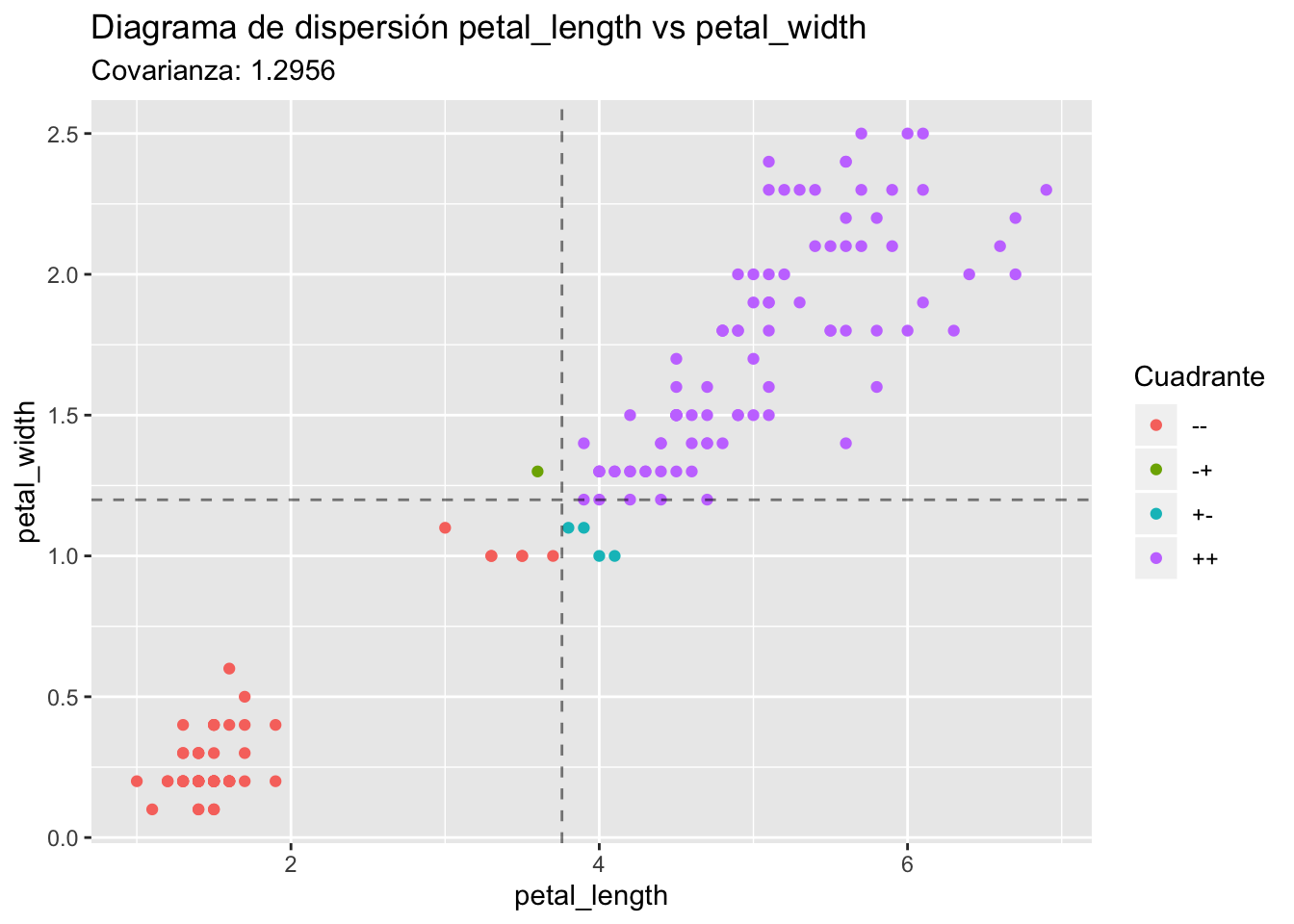
Si dibujamos el mismo gráfico agregando líneas para ˉX y ˉY, tendríamos algo como esto:
Para X comparamos con la línea vertical:
- (xi−ˉX) es positivo a la derecha
- (xi−ˉX) es negativo a la izquierda
Para Y comparamos con la línea horizontal:
- (yi−ˉY) es positivo arriba
- (yi−ˉY) es negativo abajo
La mayoría de los puntos están en los cuadrantes “++” y “–”, y en estos cuadrantes (xi−ˉX)(yi−ˉY) es positivo; por eso la covarianza es positiva.
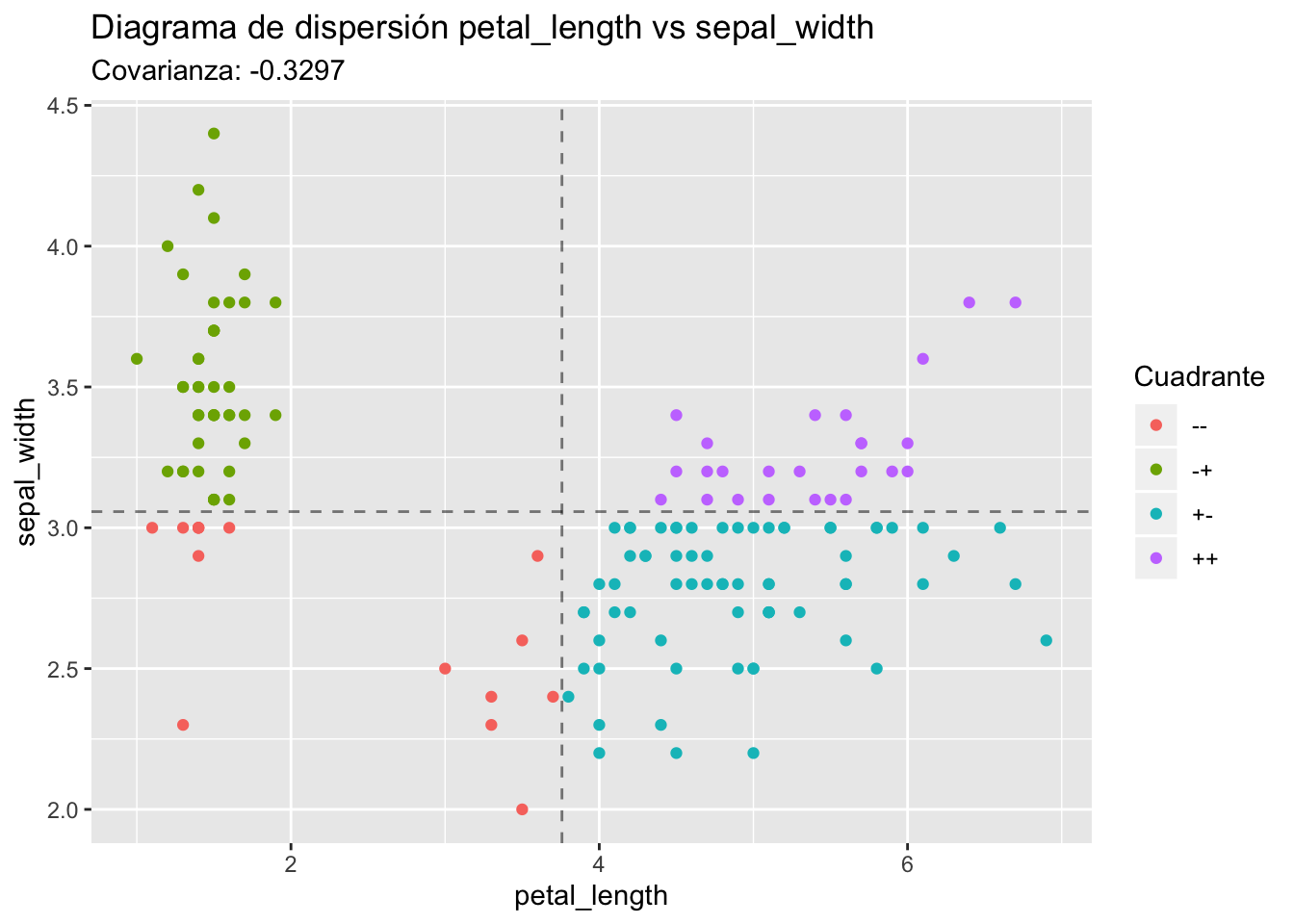
Veamos otro caso:
Ahora la mayoría de los puntos están en los cuadrantes “+-” y “-+”, y en esos cuadrantes (xi−ˉX)(yi−ˉY) es negativo, así que tendremos una covarianza negativa.
Paradoja de Simpson
Es posible que este último sea un ejemplo de la paradoja de Simpson, en la que la relación entre variables cambia drásticamente cuando se observa dentro de distintos grupos en lugar de observarla en la muestra completa.
La covarianza entre petal_length y sepal_width es -0.3296564 cuando la calculamos usando todos los datos. Veamos qué sucede cuando agrupamos por species.
iris %>%
group_by(species) %>%
summarise(
cov_petal_length__sepal_width = cov(petal_length, sepal_width)
)## # A tibble: 3 x 2
## species cov_petal_length__sepal_width
## <fct> <dbl>
## 1 setosa 0.0117
## 2 versicolor 0.0827
## 3 virginica 0.0714Y ahora todas las covarianzas de petal_length con sepal_width dentro de cada grupo de species son positivas. Por esta razón, es importante visualizar los datos antes de interpretar un estadístico. Otros ejemplos de por qué es sugerible visualizar los datos lo puedes encontrar en el famoso cuarteto de Ansconbe.
En el marco del aprendizaje automático o machine learning, también es importante analizar las variables que puedan tener un impacto sobre la variable dependiente; saber cuáles variables son potencialmente relevantes requiere conociemiento del tema sobre el que se está modelando.