Correlación
Coeficiente de correlación
Aunque la covarianza nos da el signo de la relación entre dos variables, al depender de las unidades de X y de Y, no sabemos si un valor es alto o bajo; sólo sabemos el signo. Para solucionar esto, estandarizamos los valores.
Dada una muestra (x1,y1),(x2,y2),...,(xn,yn), calculamos la correlación entre X e Y, y la denotamos por rXY al cociente de la covarianza dividida entre el producto de las desviaciones típicas.
rXY=SXYSXSY
Pregunta
Este estadístico, también conocido como Coeficiente de correlación de Pearson se encuentra entre -1 y 1.
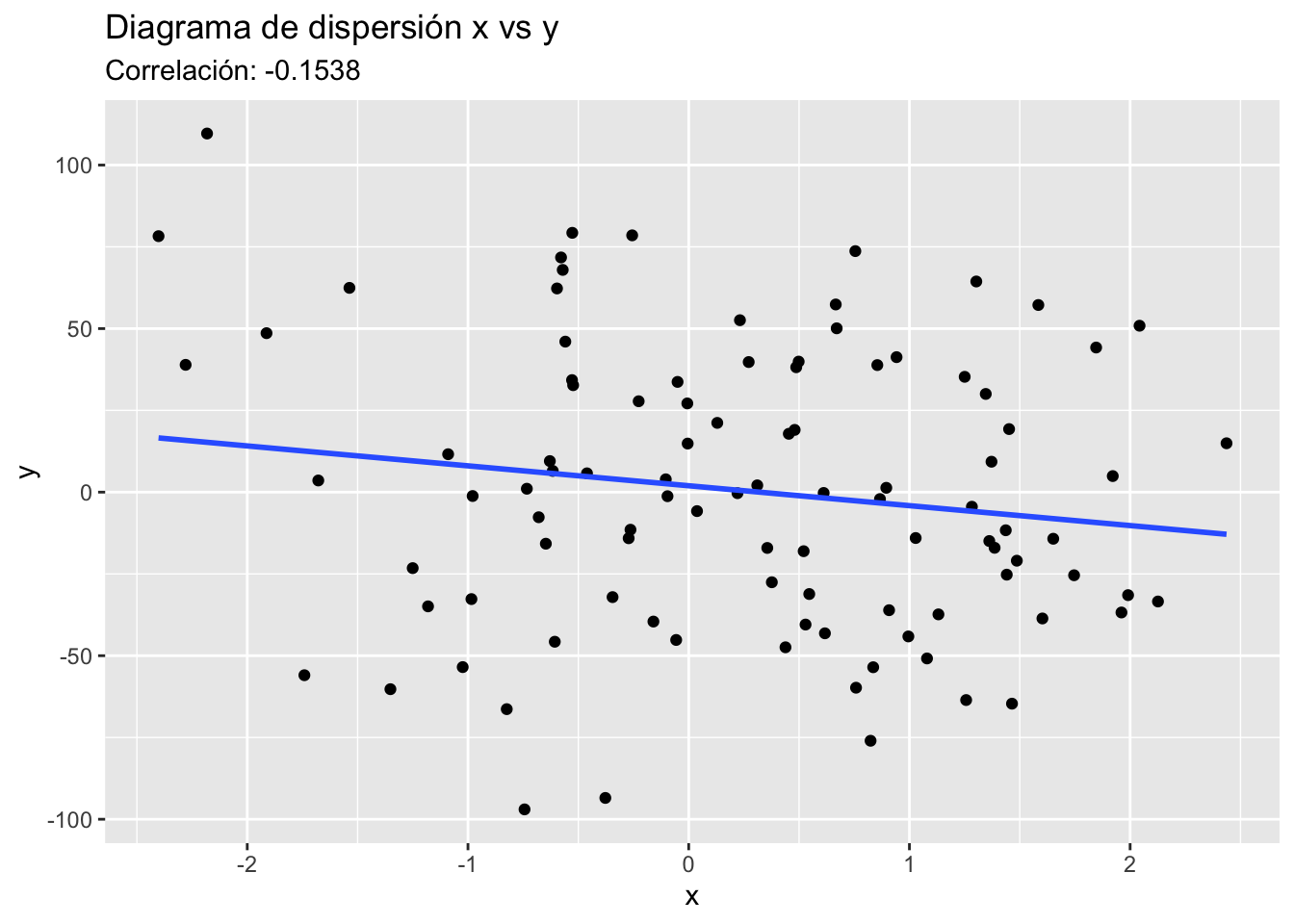
Sin relación lineal o con relación lineal débil
- rXY es igual o cercano a cero
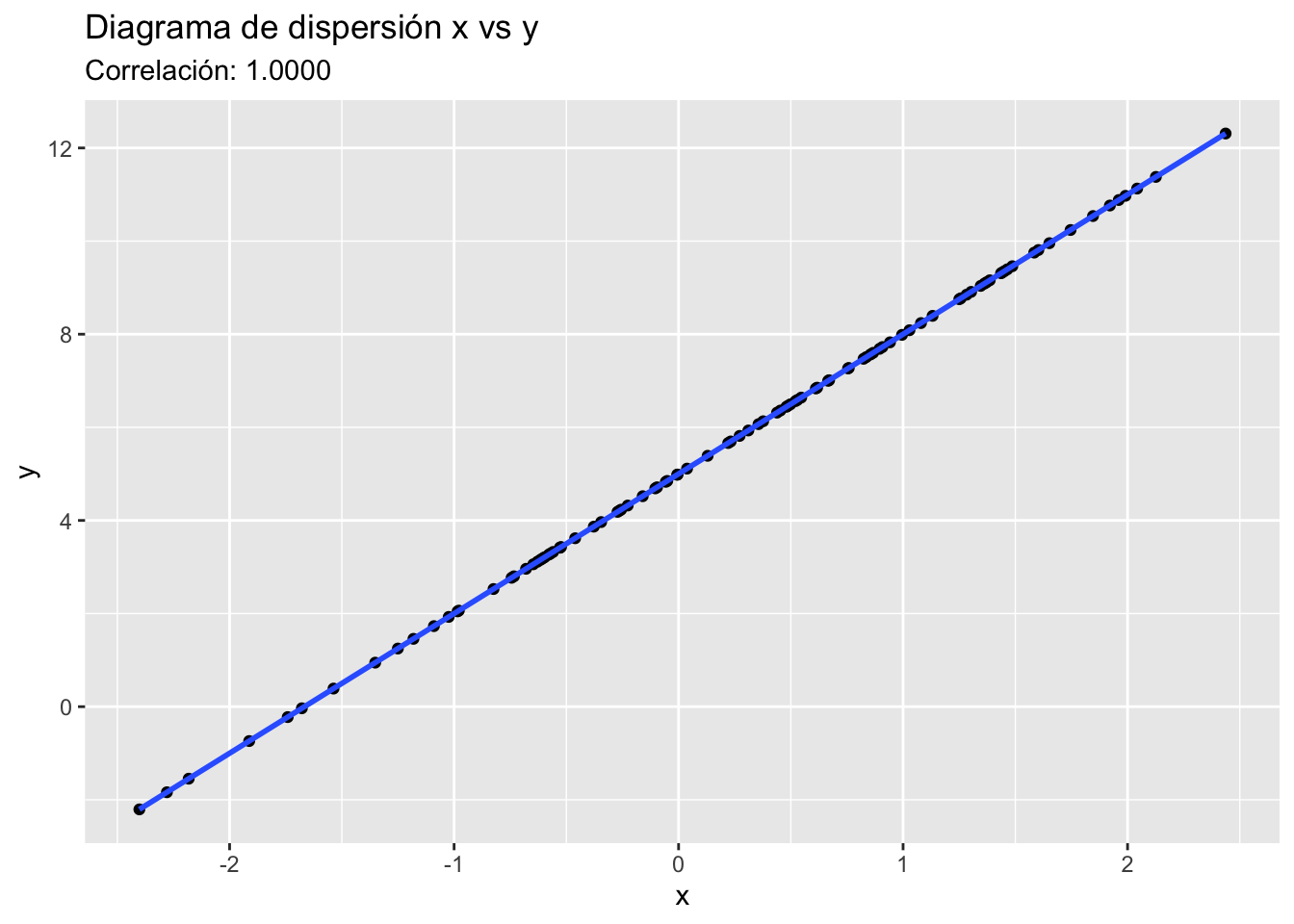
Relación lineal directa y fuerte
- rXY es igual o cercano a 1
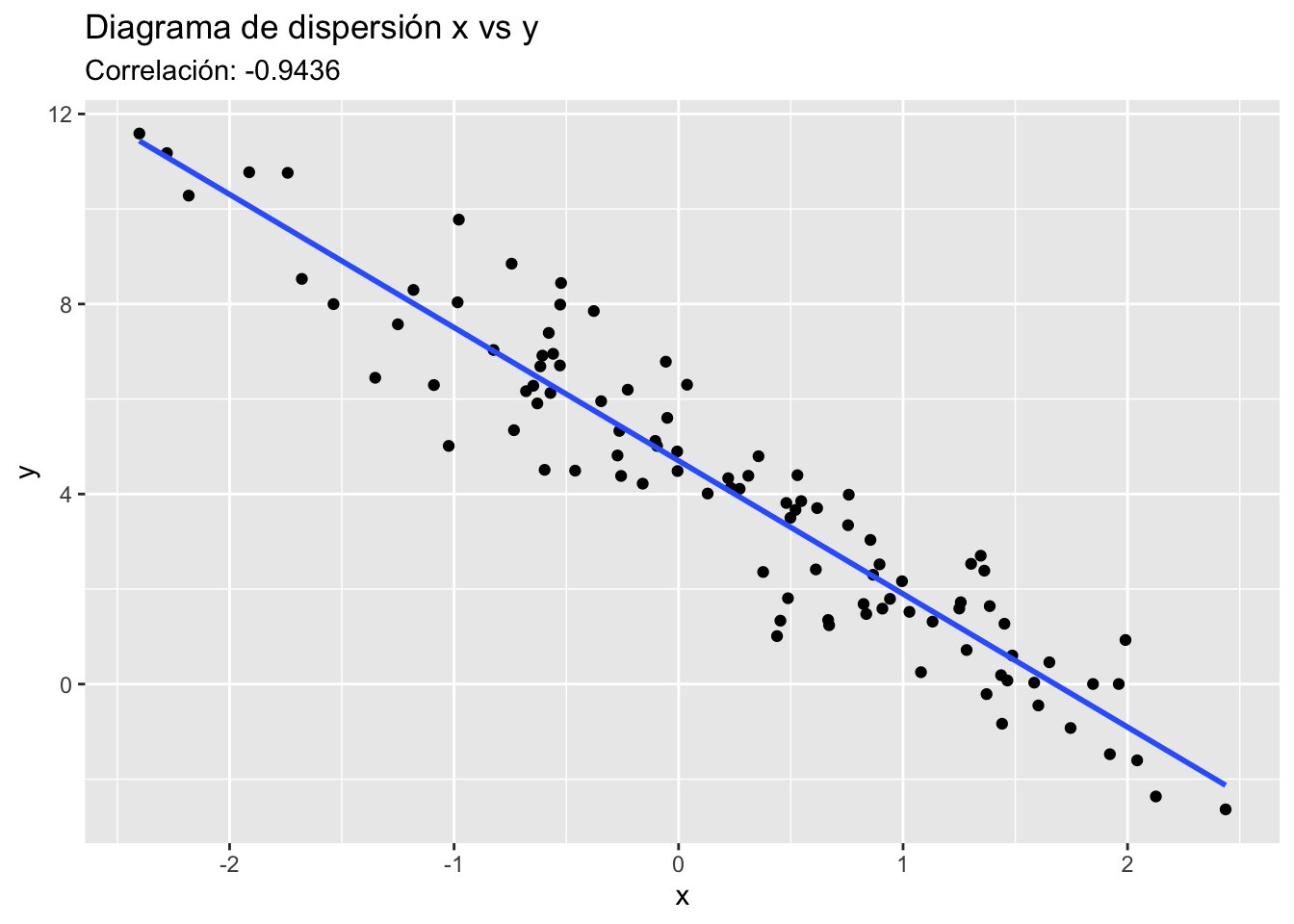
Relación lineal inversa y fuerte
- rXY es igual o cercano a -1
Existen escalas para interpretar la correlación como débil, moderada o fuerte. Sin embargo, estas escalas son subjetivas. La definición de una correlación débil o fuerte depende de cada caso. El mismo valor podría interpretarse como débil o fuerte según la situación.
Cuando una variable es una transformación lineal de otra, la correlación es perfecta. Por ejemplo, si tienes dos variables, una que mide distancia recorrida en cierto tiempo y otra que mide velocidad (asumiendo que la velocidad es constante en ese mismo tiempo), el coeficiente de correlación será 1.
Cálculo de la correlación en R
Vamos a limpiar nuestros datos para luego hacer los cálculos en R.
library(dplyr)
library(janitor)
iris <- iris %>% as_tibble() %>% clean_names()En R utilizamos la función cor para calcular la correlación
iris %>%
summarise(
cor_petal_length__petal_width = cor(petal_length, petal_width),
cor_petal_length__sepal_width = cor(petal_length, sepal_width)
)## # A tibble: 1 x 2
## cor_petal_length__petal_width cor_petal_length__sepal_width
## <dbl> <dbl>
## 1 0.963 -0.428Pregunta
petal_length y sepal_width?
- Relación directa y fuerte
- Relación directa y debil
- Relación inversa y fuerte
- Relación inversa y moderada
Propiedades de la correlación
Dada una muestra (x1,y1),(x2,y2),...,(xn,yn), se cumplen las siguientes propiedades relacionadas con la correlación rXY:
- Si se transforman linealmente las variables X, Y mediante X′=a+bX y Y′=c+dY, la correlación entre X′ e Y′, rX′Y′ será la correlación original multiplicada por el signo de bd, siempre que b≠0 y d≠0.
rX′Y′=bd|bd|rXY
iris %>%
summarise(
cor_1 = cor(petal_length, petal_width),
cor_2 = cor(1 + 2*petal_length, 3 - 4*petal_width)
)## # A tibble: 1 x 2
## cor_1 cor_2
## <dbl> <dbl>
## 1 0.963 -0.963- La correlación de una variable consigo misma es 1
iris %>%
summarise(
cor_1 = cor(petal_length, petal_length)
)## # A tibble: 1 x 1
## cor_1
## <dbl>
## 1 1.000- La correlación entre X e Y es igual a la correlación entre Y y X
iris %>%
summarise(
cor_1 = cor(petal_length, petal_width),
cor_2 = cor(petal_width, petal_length)
)## # A tibble: 1 x 2
## cor_1 cor_2
## <dbl> <dbl>
## 1 0.963 0.963Pregunta
Cómo se ve la correlación
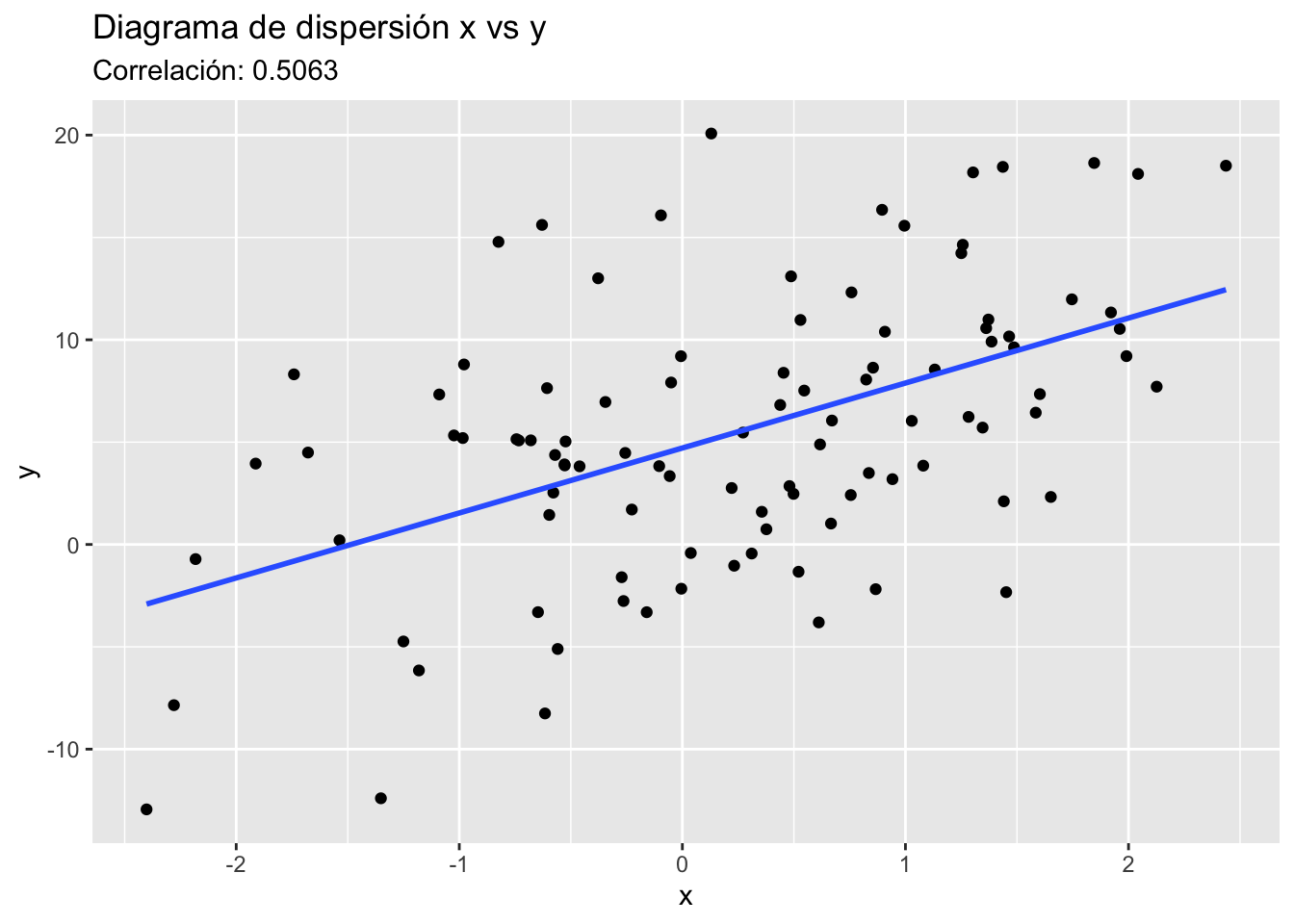
Además de identificar en cuáles cuadrantes está la mayoría de los puntos de un diagrama de dispersión, el coeficiente de correlación mide qué tan cerca están los puntos de una línea recta que refleja la tendencia de los datos. Mientras más cercanos estén a esa línea, mayor será el valor absoluto de rXY.
Te dejo un link para que juegues a adivinar la correlación de un diagrama de dispersión en Guess the correlation.
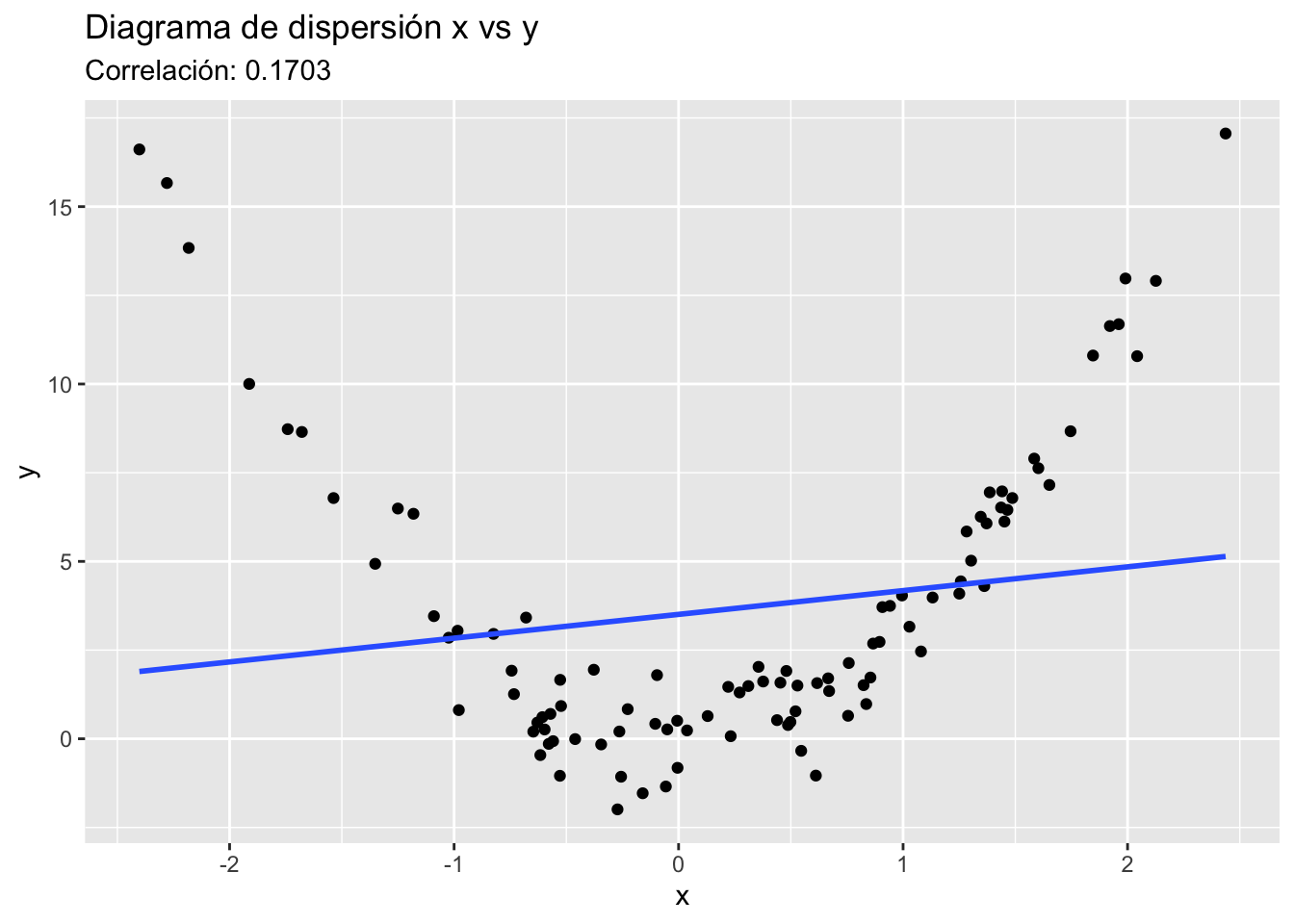
Relaciones no lineales
Es importante resaltar que la covarianza y el coeficiente de correlación no detectan relaciones no lineales entre las variables. Por ejemplo, si la relación entre X e Y es cuadrática (o polinímica de mayor órden), logarítmica, exponencial, etc., podríamos tener un coeficiente de correlación cercano a 0, pero esto no significaría que no hay relación entre X e Y; sólo significa que no hay relación lineal entre estas variables.
¡Pero no te preocupes! Hay métodos estadísticos para analizar este tipo de relaciones, sólo que son más avanzados y los cubriremos más adelante.