Asimetría y kurtosis
Las medidas de asimetría sirven para tener una idea acerca de la forma de una distribución de frecuencias con sólo un número. Por supuesto, para realmente conocer la forma de la distribución es mejor graficarla, pero tener un número que nos permita tomar esta decisión puede ser útil; por ejemplo, si necesitamos que un programa tome una decisión dependiendo de la forma de la distribución.
Asimetría
Formalmente, decimos que una distribución de frecuencias es simétrica si la media aritmética \(\bar{X}\) es igual a la mediana \(Md\). Esto significa que en cualquier otro caso, la distribución es asimétrica.
Hay algunas definiciones más gráficas de la asimetría, pero en mi opinión son muy ambiguas y consideran demasiados casos, como por ejemplo si la distribución es multi-modal o no. Por simplicidad, vamos a mantener esta definición que compara la mediana con la media y que realmente sirve en la mayoría de los casos.
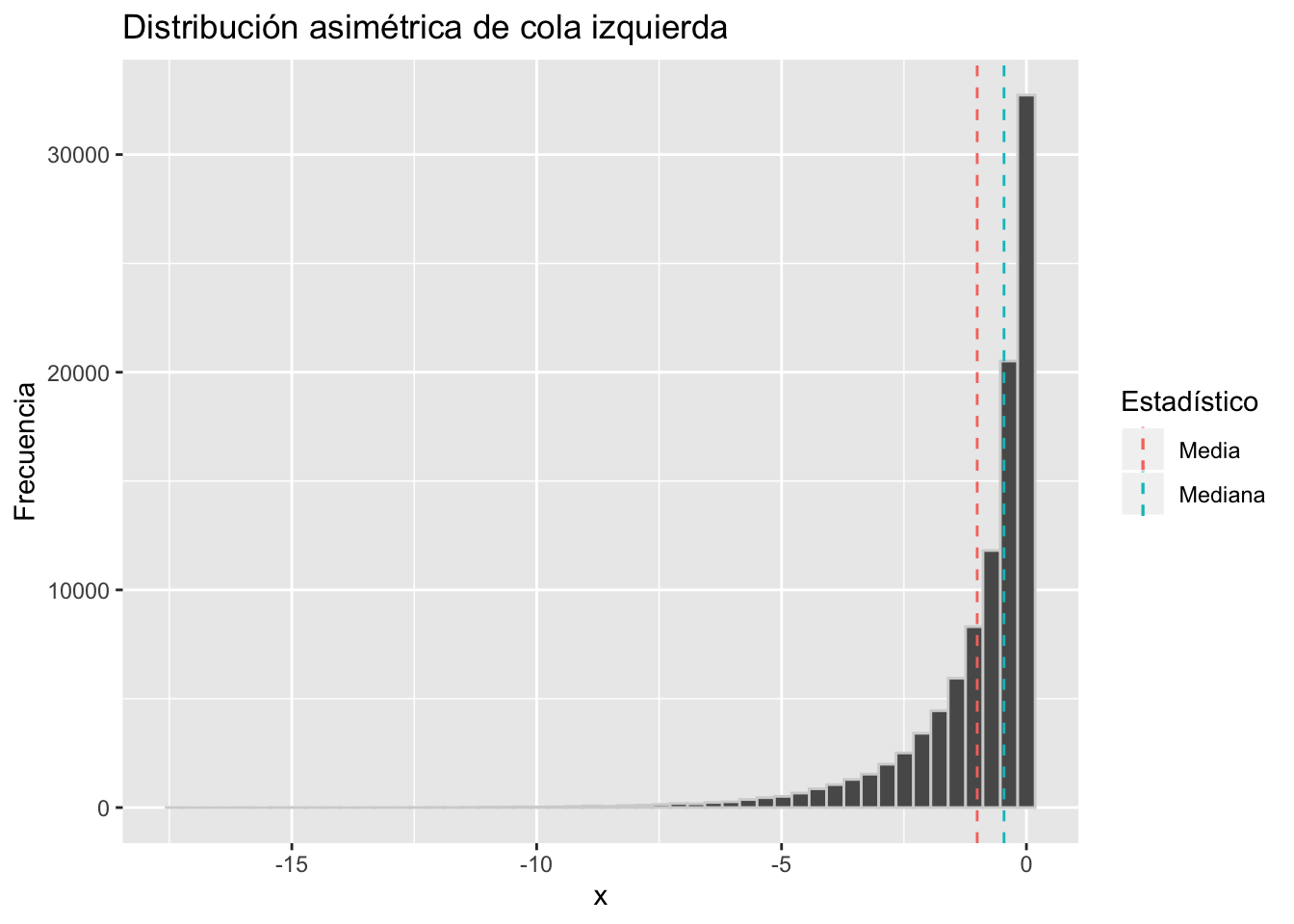
- Cuando \(\bar{X} < MD\) decimos que la distribución es Asimétrica a la izquierda, Asimétrica de cola izquierda o que tiene Asimetría negativa
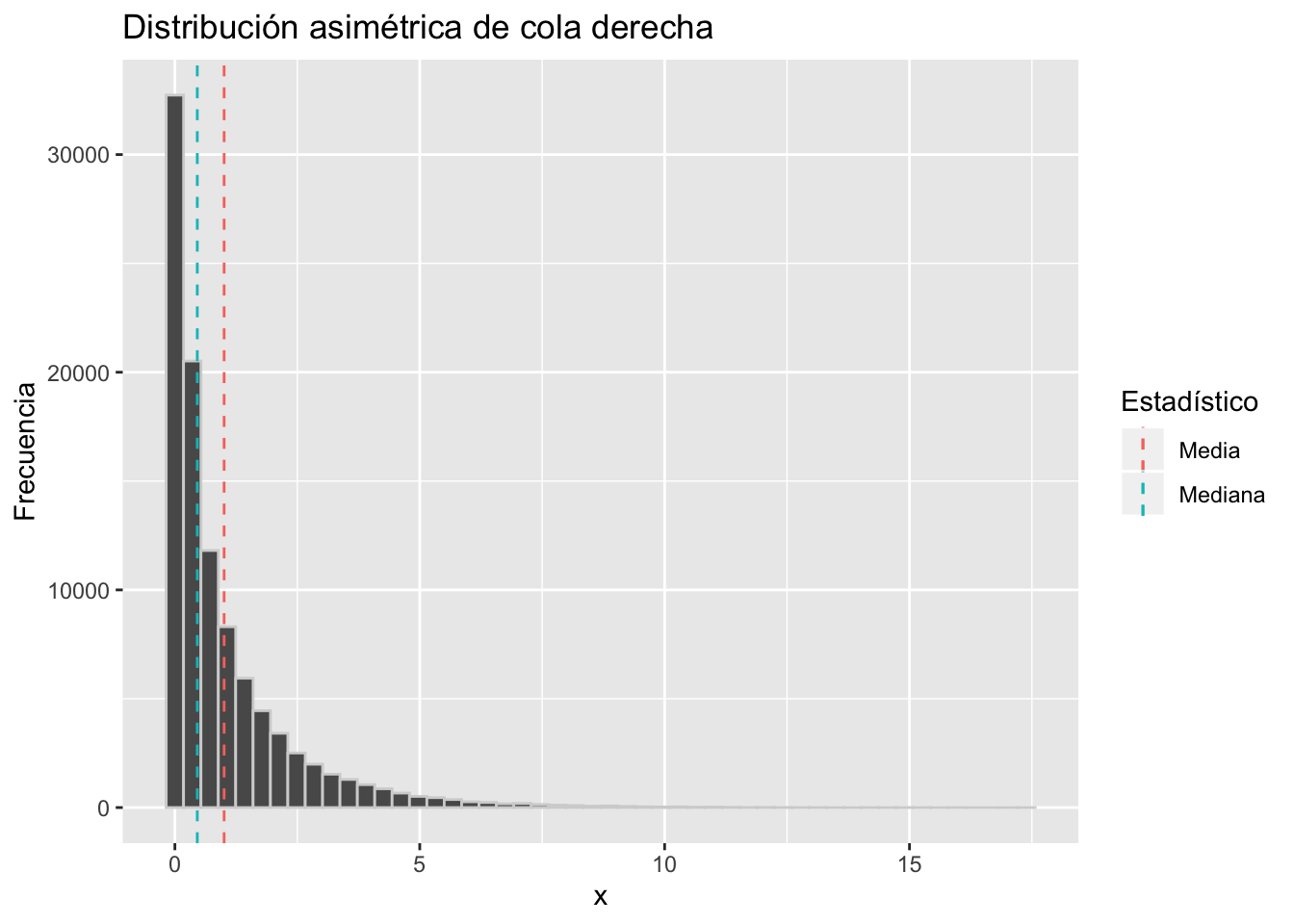
- Cuando \(\bar{X} > MD\) decimos que la distribución es Asimétrica a la derecha, Asimétrica de cola derecha o que tiene Asimetría positiva
¿Cómo se ve la asimetría?
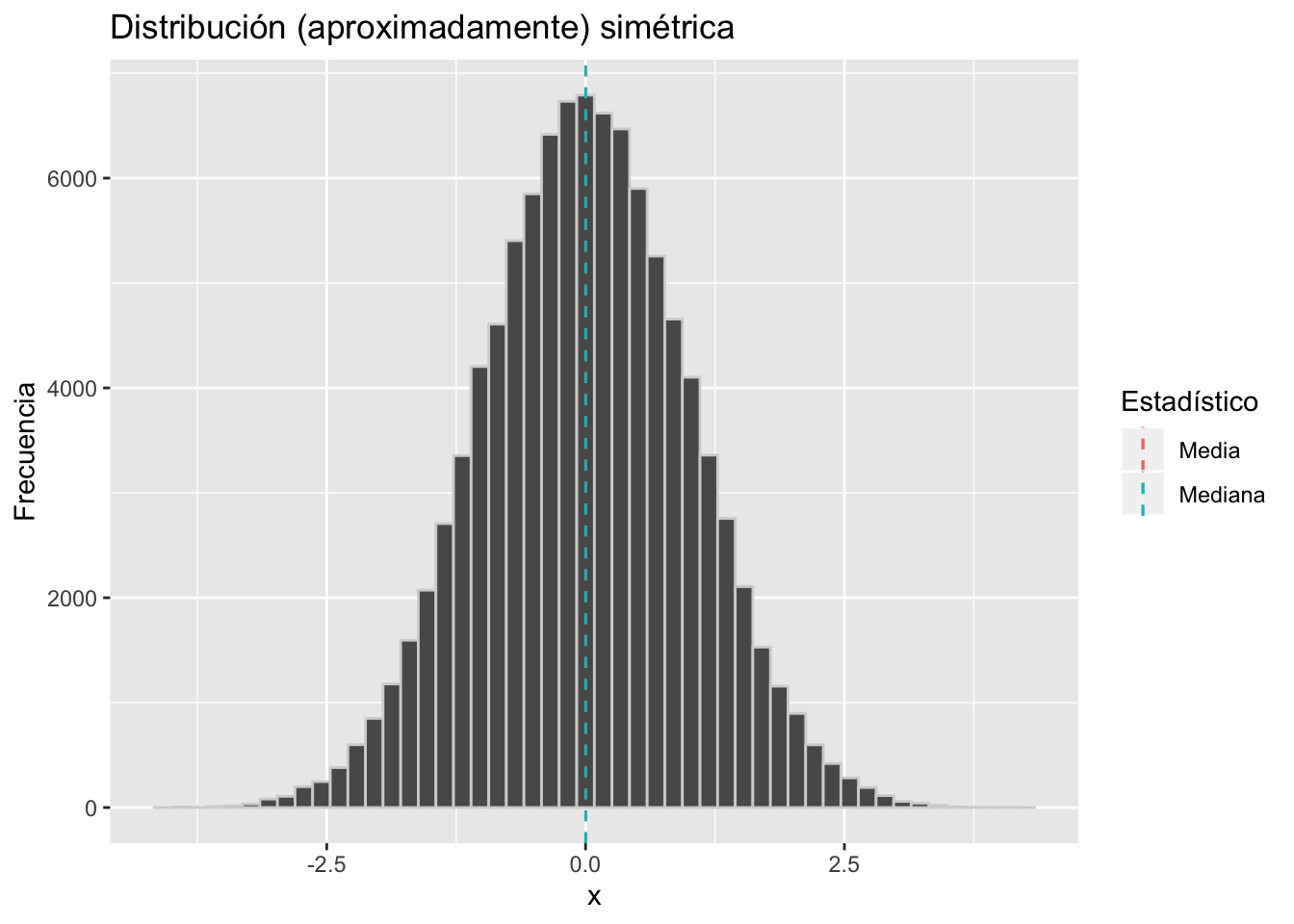
Conectemos estos gráficos con la definición. Por un lado tenemos que para una distribución simétrica, el histograma se ve simétrico: pareciera que hubiese un espejo justo donde está la media.
Más allá de esto, lo que sucede es que la media es suceptible a valores extremos mientras que la mediana es más resistente, o técnicamente, más robusta. En el ejemplo de la distribución asimétrica a la derecha, esos pocos valores altos halan la media hacia la derecha, mientras que no afectan a la mediana.
Pregunta
- Simétrica (hay aproximadamente la misma cantidad de hogares con ingresos bajos que altos)
- Asimétrica a la izquierda (muchos hogares con ingresos altos, pocos hogares con ingresos bajos)
- Asimétrica a la derecha (muchos hogares con ingresos bajos, pocos hogares con ingresos alto)
Pregunta
Pista: Recuerda que la media es más suceptible a valores atípicos que la mediana.
En una muestra, es prácticamente imposible tener simetría perfecta. Por esto, no basta con saber el signo de la asimetría, sino también la magnitud de esta. Para eso utilizamos los llamados Coeficientes de asimetría.
Coeficiente de asimetría basado en momentos
También conocido como el coeficiente de asimetría de Fisher-Pearson, se basa en momentos centrales:
\[ asimetría = \frac{m_3}{S^3} \] Donde \(S^3\) es la desviación típica elevada al cubo y \(m_r\) es lo que se conoce como el Momento central de orden \(r\), donde \(r\) puede ser cualquier entero positivo y se calcula se la siguiente manera.
\[ m_r = \frac{1}{n} * \sum_{i=1}^{n}(x_i - \bar{X})^r \]
Pregunta
¿Cuál es el valor del momento central de orden 1?
- No se puede saber. Es distinto para cada variable
- 1
0
Interpretación:
- \(asimetría = 0\): Distribución simétrica
- \(asimetría > 0\): Distribución asimétrica a la derecha
- \(asimetría < 0\): Distribución asimétrica a la izquierda
Evidentemente, la varianza también es un momento central, pero de orden 2. Por esto es que decimos que este coeficiente de asimetría está basado en momentos.
Analizando la fórmula podemos entender a nivel intuitivo de qué se trata. Por una parte, dividir entre \(S^3\) sirve para estandarizar los valores.
\[ \frac{m_3}{S^3} = \frac{1}{n} * \sum_{i=1}^{n}\left( \frac{x_1-\bar{X}}{S} \right)^3 = \frac{1}{n} * \sum_{i=1}^{n}z_i^3 \]
Es decir, el coeficiente de asimetría es el momento central de orden 3 para los datos estandarizados.
Pregunta
- Media = 0, Varianza = 1
- Media = 1, Varianza = 0
- Media = 1, Varianza = 1
- Es distinto para cada variable
Y finalmente, elevar los valores estandarizados a una potencia impar tiene estos efectos:
- Si el valor absoluto de \(z_i\) está entre 0 y 1, \(z_i^3\) se acercará más al 0
- Si el valor absoluto de \(z_i\) es mayor a 1, \(z_i^3\) se alejará del 0
De esta forma, un valor positivo indica que hay más valores extremos positivos que negativos, y viceversa. Estos valores extremos serán finalmente los que alejen a la media de la mediana.
Cálculo en python
Vamos a descargar iris desde un repositorio público de github. Ya los nombres vienen en un formato legible y que cumple con las características del PEP8
import pandas as pd
iris = pd.read_csv("https://raw.githubusercontent.com/toneloy/data/master/iris.csv")
iris.head()## sepal_length sepal_width petal_length petal_width species
## 0 5.1 3.5 1.4 0.2 setosa
## 1 4.9 3.0 1.4 0.2 setosa
## 2 4.7 3.2 1.3 0.2 setosa
## 3 4.6 3.1 1.5 0.2 setosa
## 4 5.0 3.6 1.4 0.2 setosaPara calcular la asimetría, utilizamos el método .skew().
iris.skew()## sepal_length 0.314911
## sepal_width 0.318966
## petal_length -0.274884
## petal_width -0.102967
## dtype: float64
Internamente, pandas pandas utiliza una fórmula un poco distinta a la que describimos antes, ya que calcula un estimador insesgado de la asimetría. Sin embargo, los resultados casi siempre son muy parecidos, especialmente para muestras grandes.
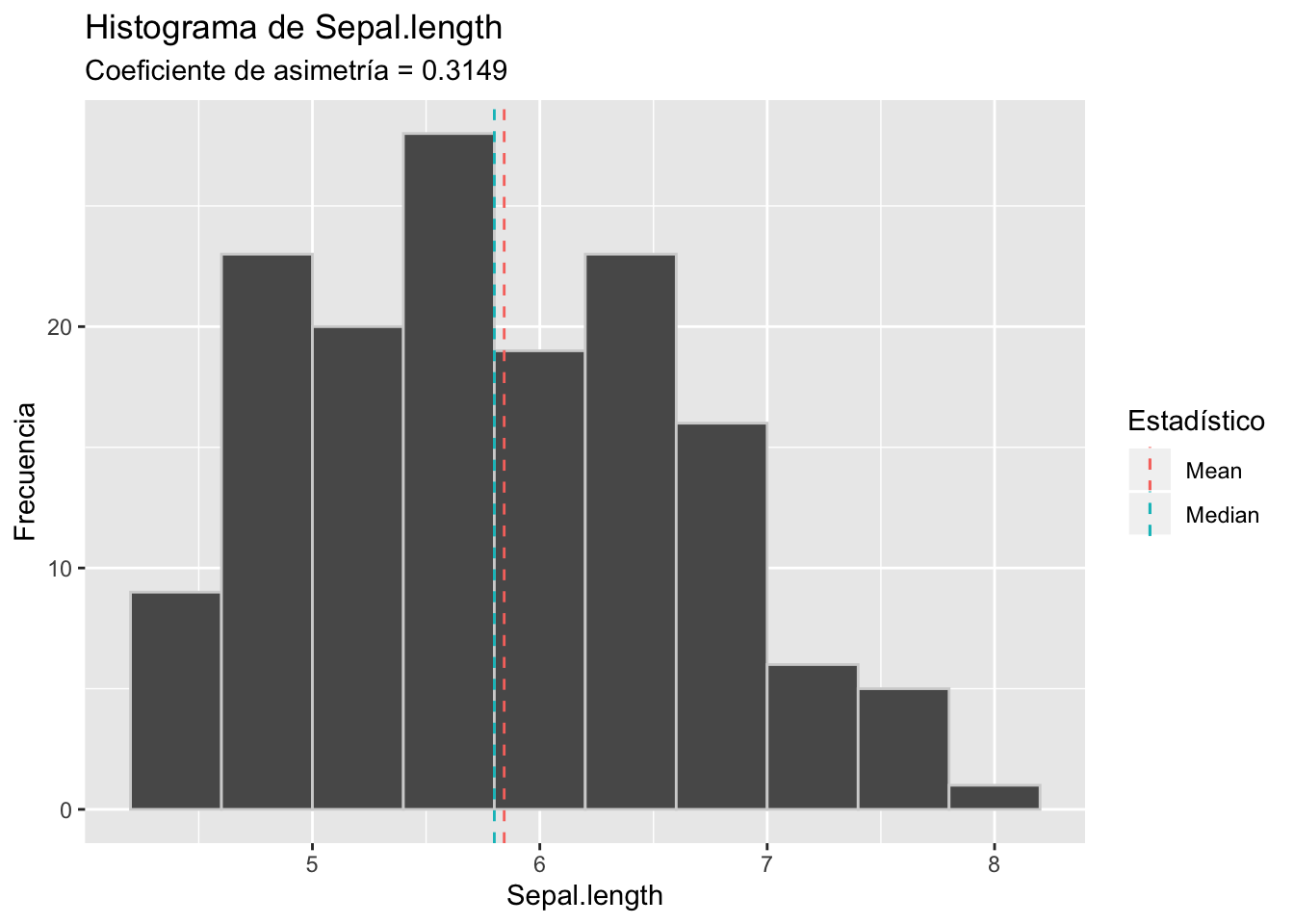
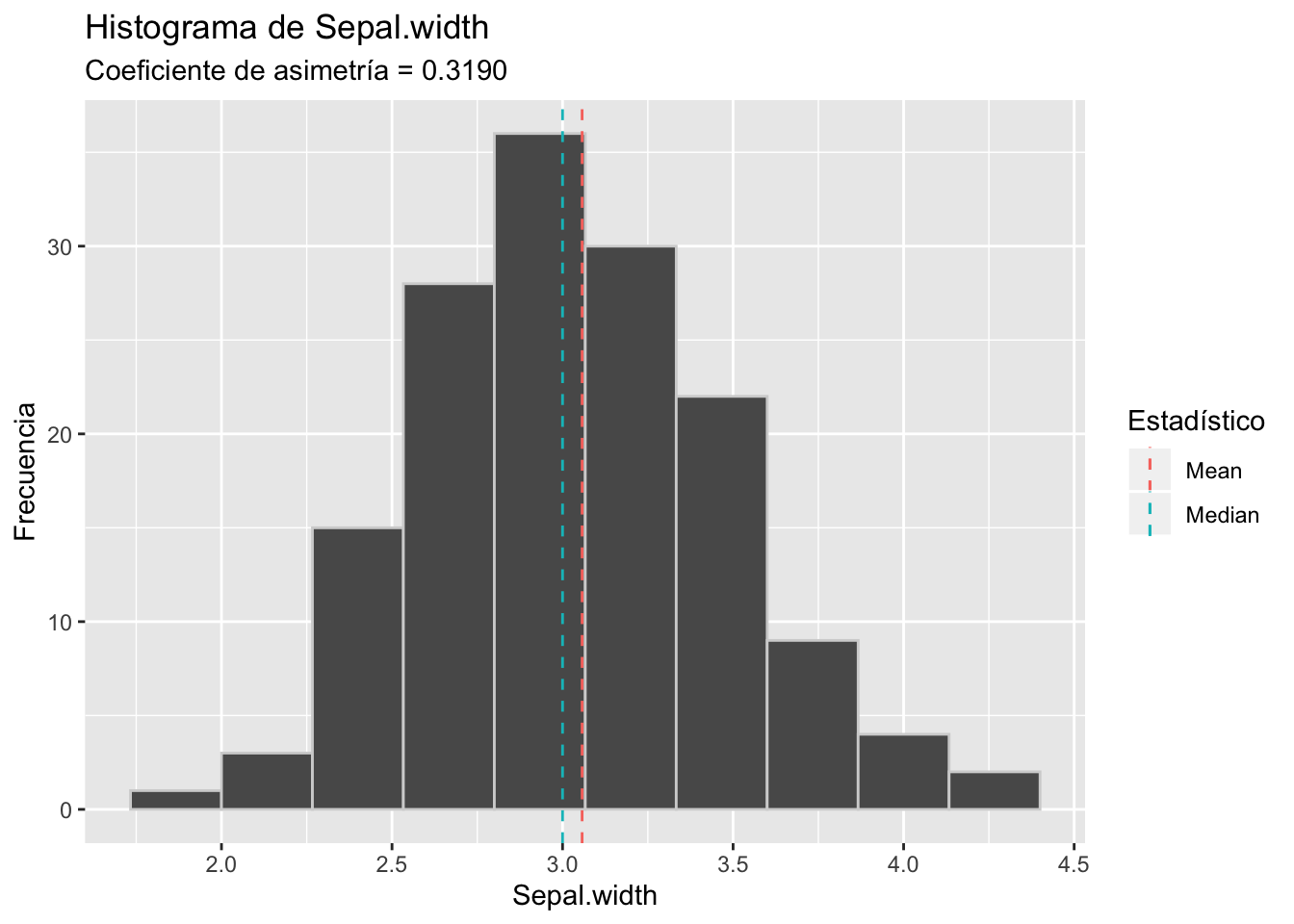
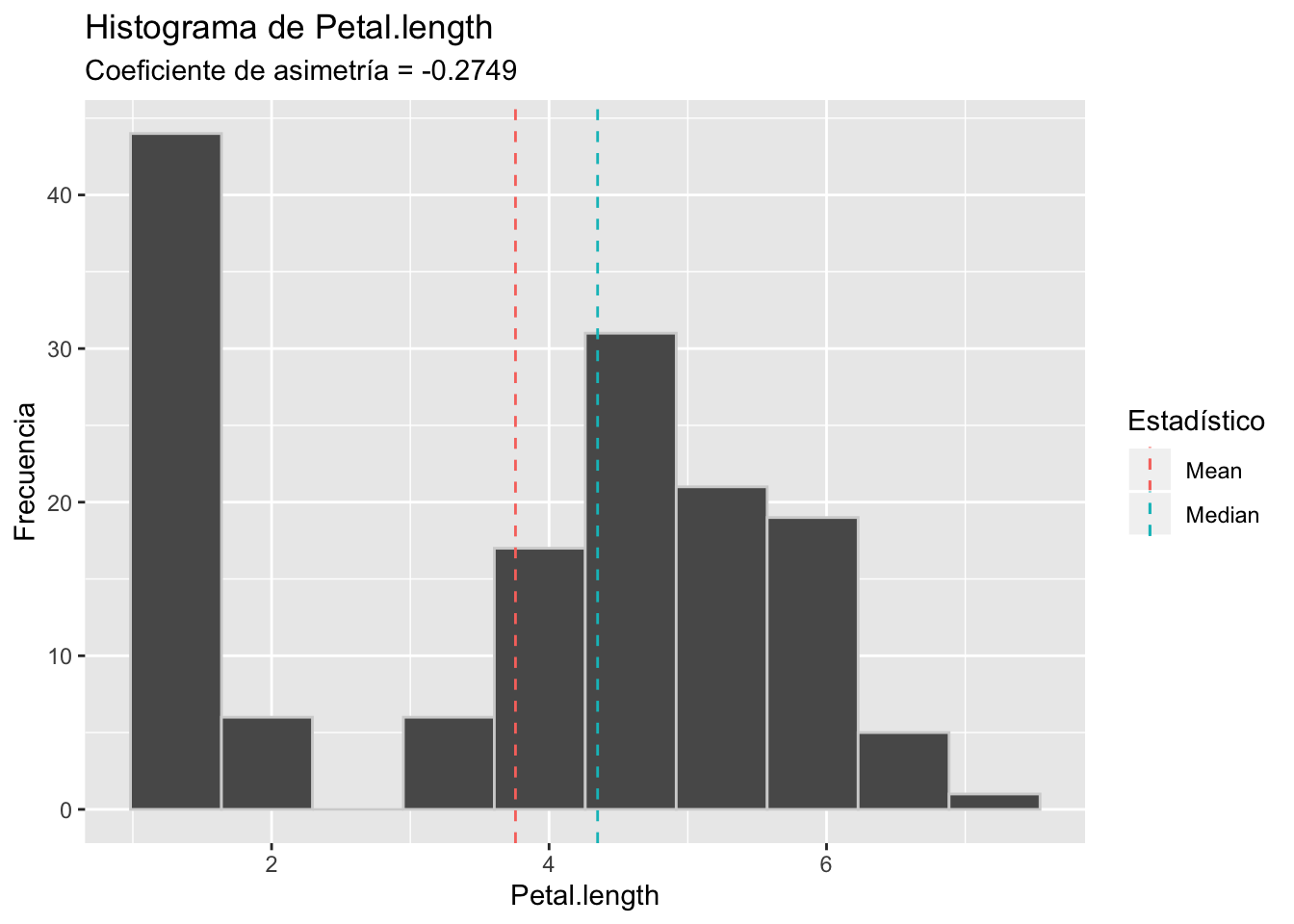
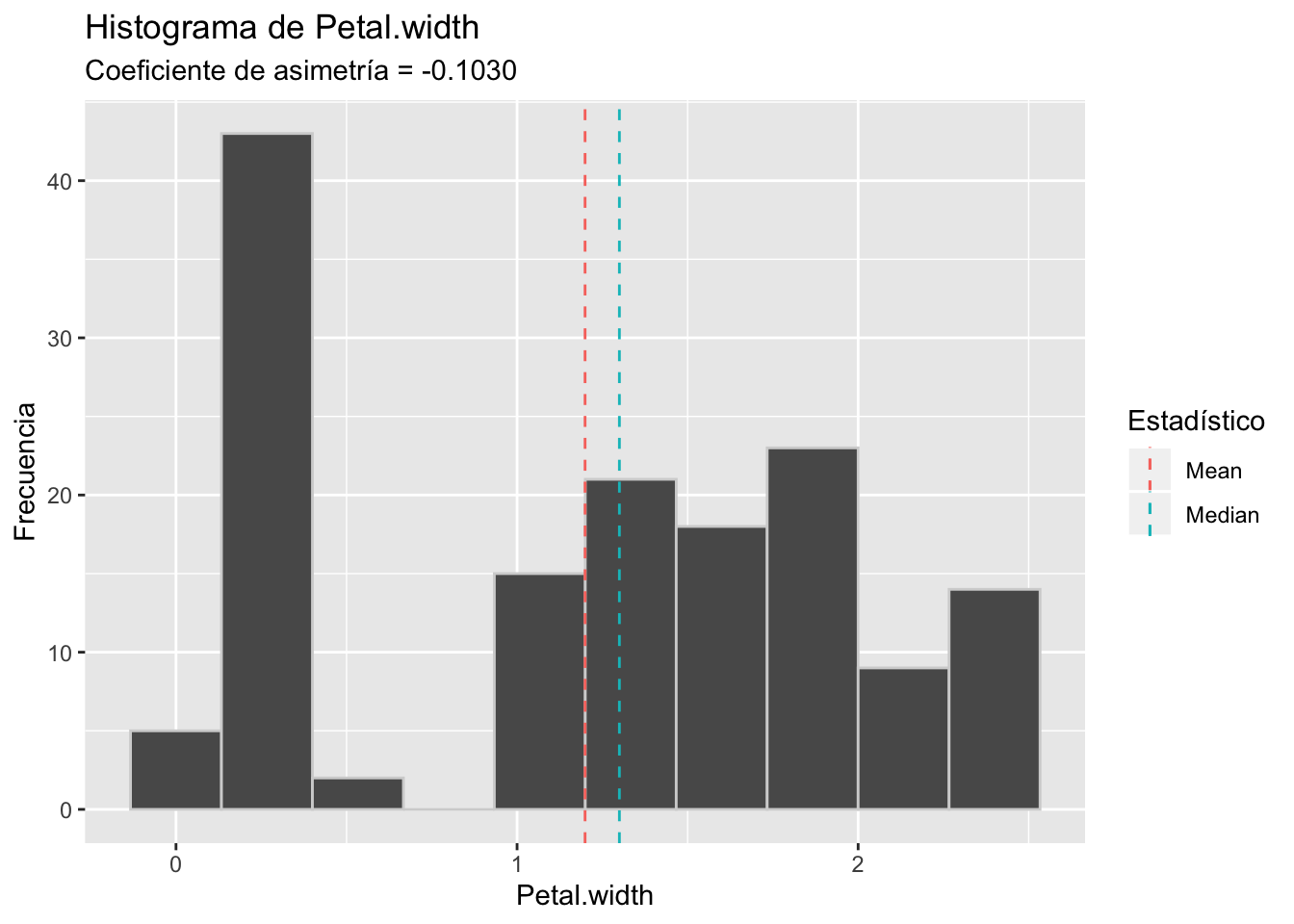
Veamos los histogramas de cada una estas variables
Como vemos, los datos reales son más complejos que la teoría, incluso estos que son batante sencillos. Dos de estos gráficos no se parecen mucho a los histogramas que graficamos al principio. Por esta razón, recuerda siempre acompañar el análisis de la asimetría con algún gráfico como un histograma, un diagrama de cajas, un polígono de frecuencias, etc.
Recuerda siempre acompañar el análisis de la asimetría con algún gráfico
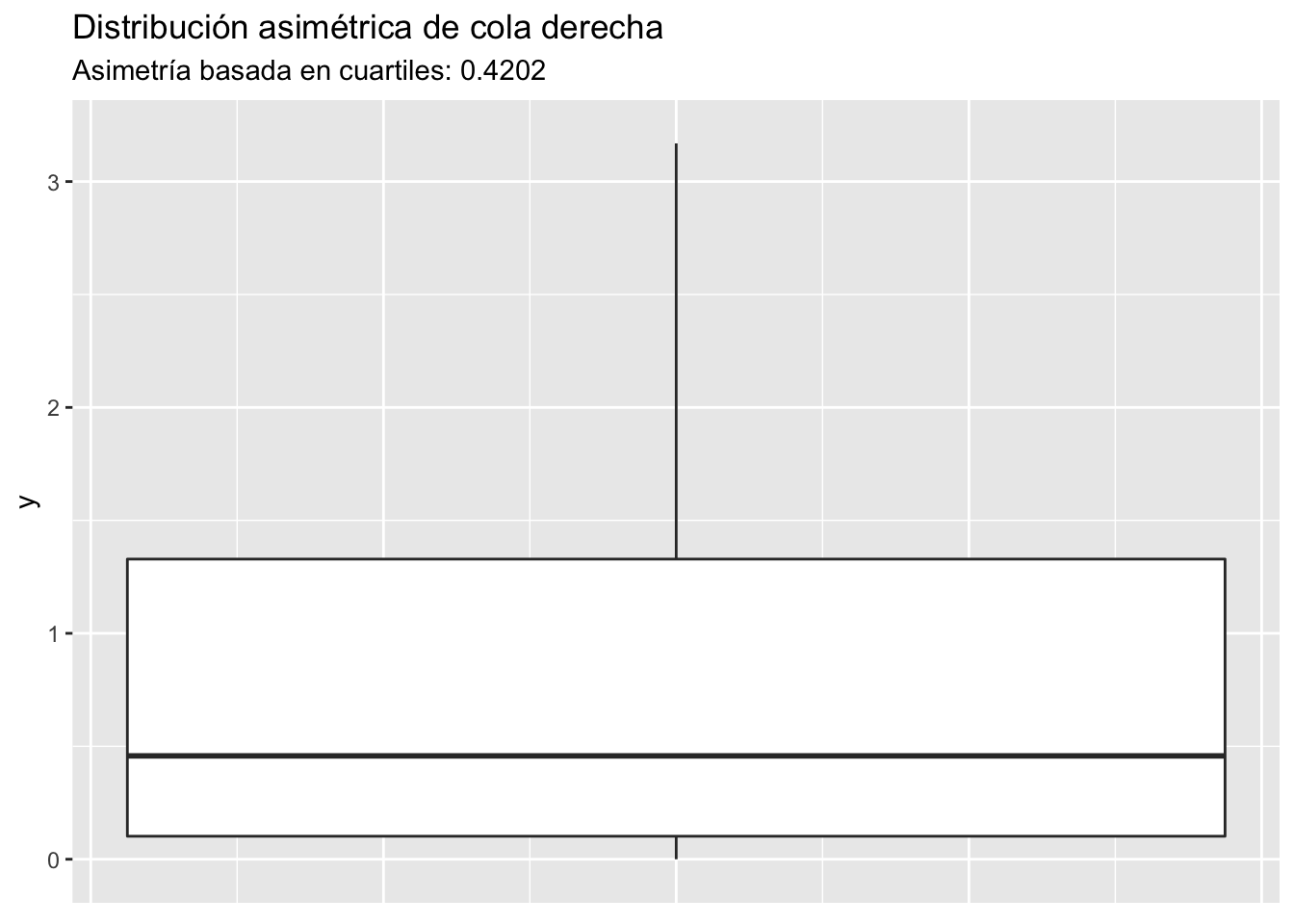
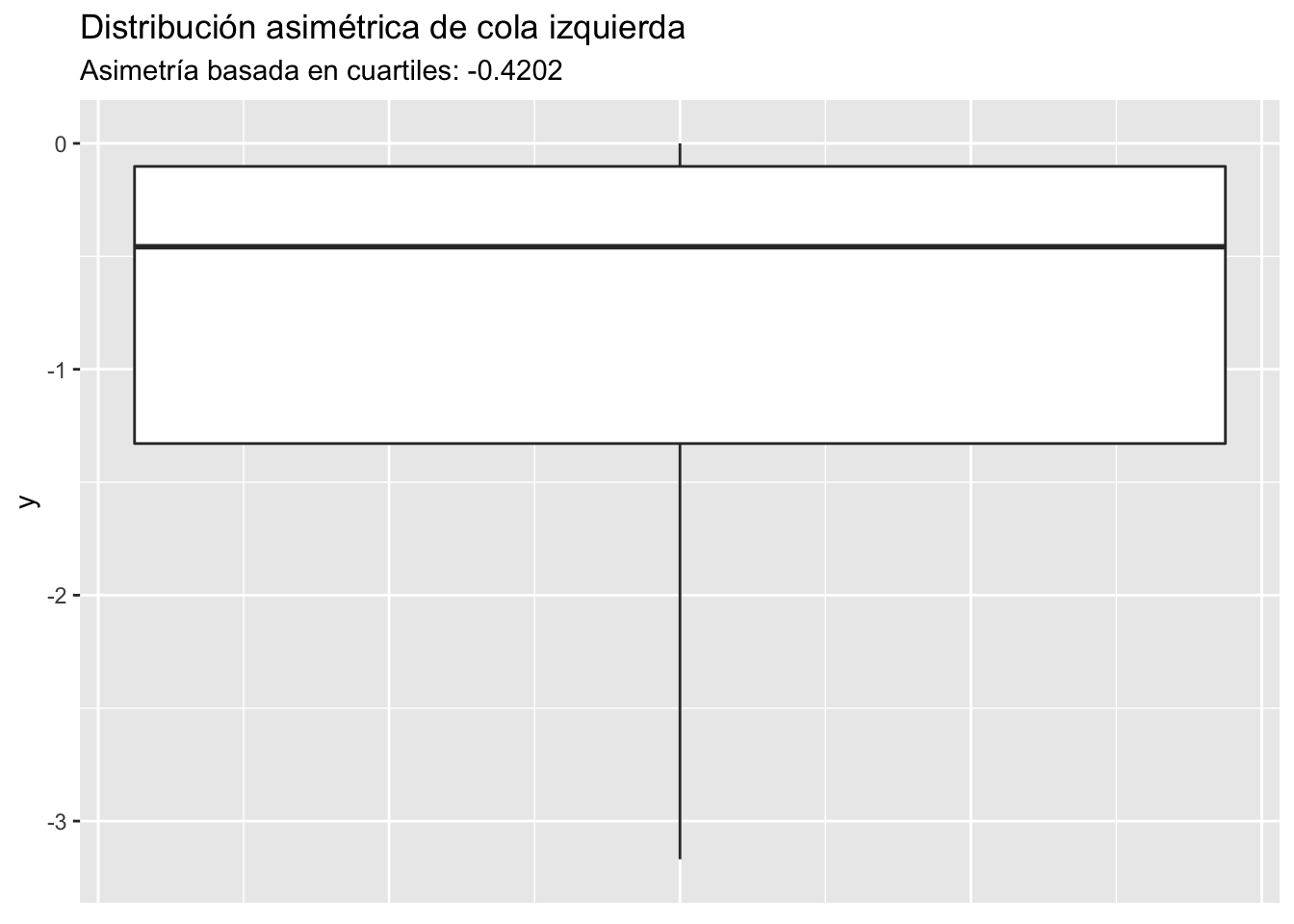
Asimetría basada en cuartiles
Otro coeficiente de asimetría es uno basado en cuartíles. Gráficamente, la idea es comparar la altura de las partes superior \((Q_3 - Q_2)\) e inferior \((Q_2 - Q_1)\) de un diagrama de caja, y normalizar el resultado dividiendo entre el \(IQR\).
\[ \frac{(Q_3 - Q_2) - (Q_2 - Q_1)}{Q_3 - Q_1} \]
La interpretación de este coeficiente es la misma que la del coeficiente basado en momentos. Comparamos con el 0 y decidimos si la distribución a simétrica o asimétrica dependiendo del signo.
Gráficamente:
- Simétrica: La parte inferior es igual a la parte superior
- Asimétrica a la derecha: La parte superior es más grande que la la parte inferior
- Asimétrica a la izquierda: La parte superior es más pequeña que la la parte inferior
Vamos a crear nuestra función para calcular este coeficiente de asimetría
def quartile_skew(x):
q = x.quantile([.25, .50, .75])
return ((q[0.75] - q[0.5]) - (q[0.5] - q[0.25])) / (q[0.75] - q[0.25])
quartile_skew(iris["sepal_length"])## -0.07692307692307661
Pregunta
Otros coeficientes de asimetría
Otras dos maneras de medir la asimetría atribuídos a Pearson son
\[ \frac{\bar{X}-Mo}{S} \]
Donde \(Mo\) es la Moda (el valor que más se repite), aunque en el caso de variables continuas, lo ideal sería calcular su valor para datos agrupados, pero eso no lo cubriremos por ahora.
La otra alternativa es directamente comparar la media con la mediana
\[ \frac{3(\bar{X}-Md)}{S} \]
Nuevamente, para interpretar estos coeficientes comparamos su valor con el cero.
Kurtosis
Otra medida que se utiliza para describir la forma de la distribución es la kurtósis o curtósis. Esta utiliza el moomento central estandarizado de orden 4 para detectar valores extremos. En presencia de valores extremos, la forma de la distribución parece más puntiaguda; por esto la kurtósis se conoce como una medida del apuntalamiento de la distribución.
Dada una muestra \(x_1, x_2, ..., x_n\), la kurtósis se calcula como
\[ \frac{m_4}{S^4} \]
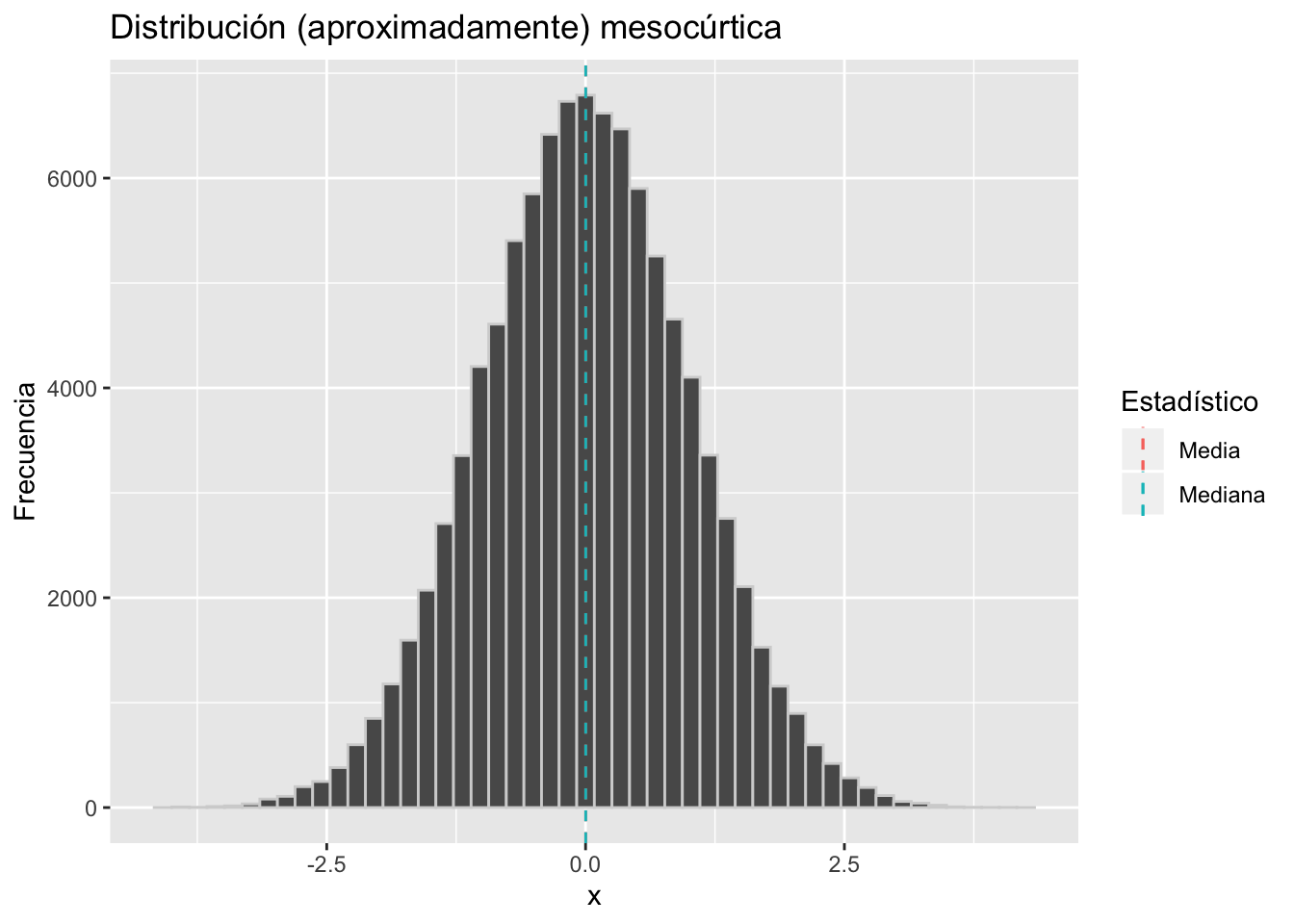
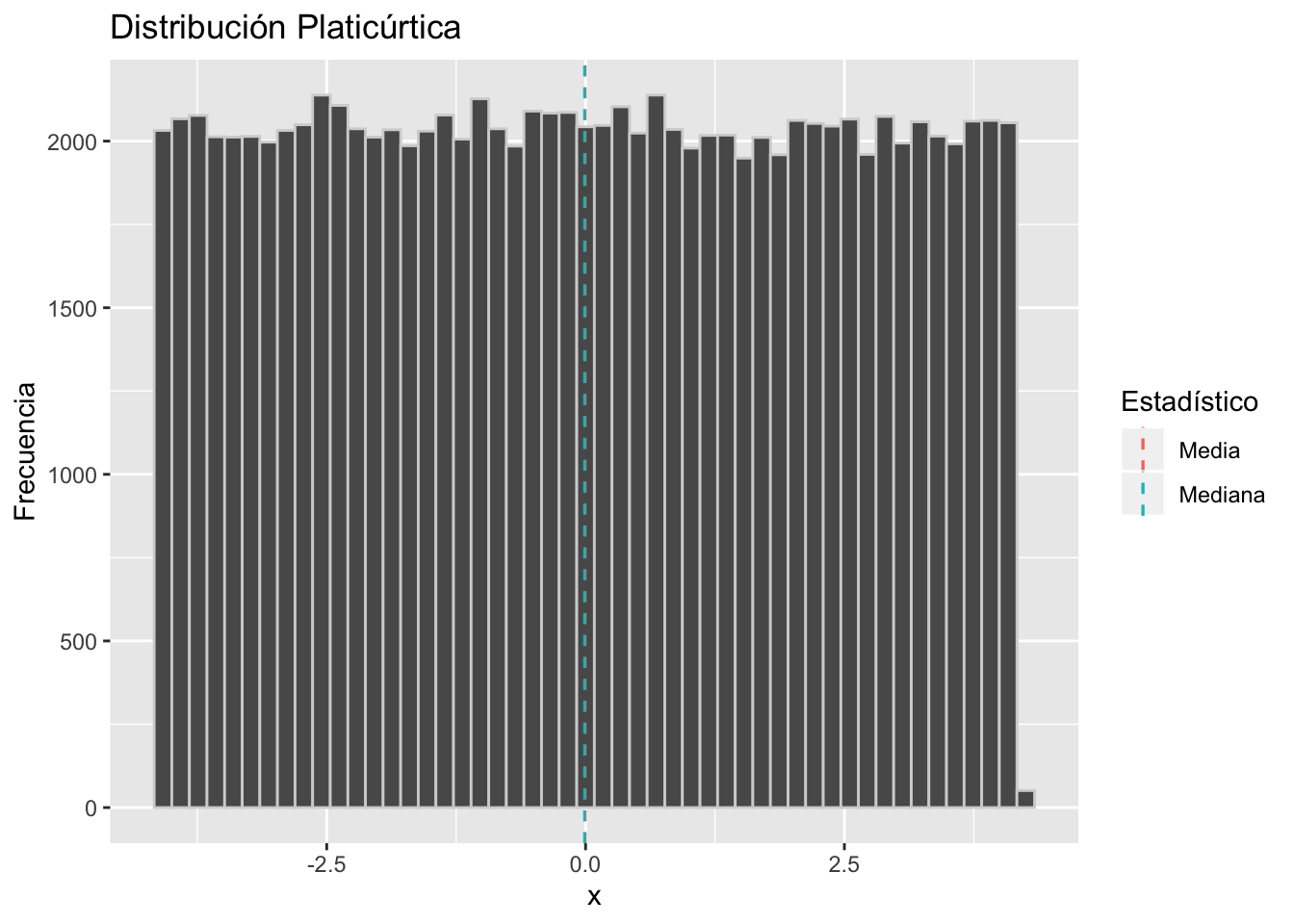
Este valor lo comparamos con 3, y dependiendo de ello, decimos que la distribución es Platicúrtica, Mesocúrtica o Leptocúrtica:
- Si \(kurtosis < 3\) la distribución es Platicúrtica
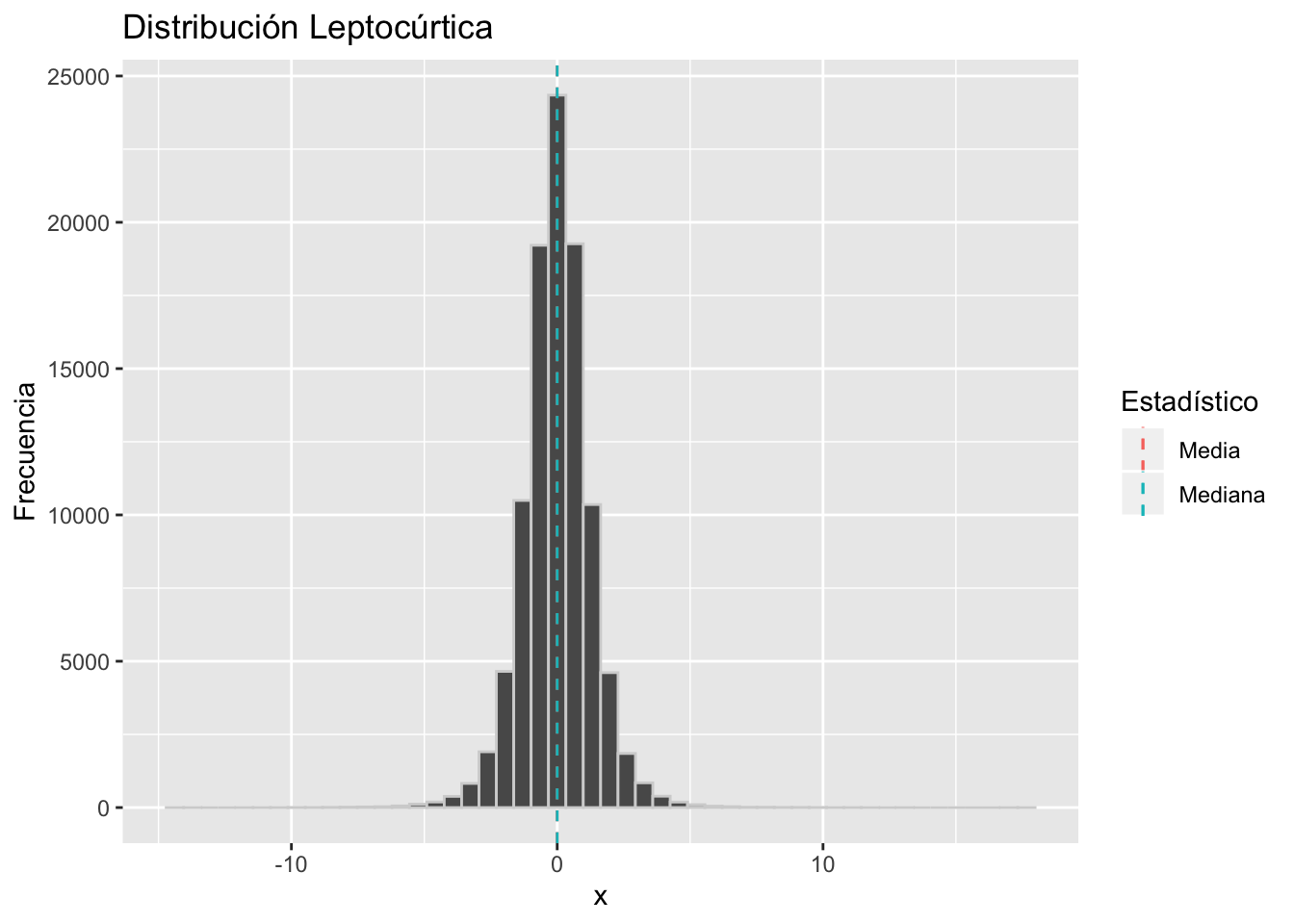
- Si \(kurtosis = 3\) la distribución es Mesocúrtica
- Si \(kurtosis > 3\) la distribución es Leptocúrtica
Para los estudiosos o los que tengan el suficiente conocimiento de teoría de la probabilidad, comparamos la kurtosis con 3 porque este es el valor la kurtosis para la distribución \(N(\mu, \sigma^2)\).
Al igual que con la asimetría basada en momentos, podemos llegar a una expresión basada en los datos estandarizados.
\[ \frac{m_4}{S^4} = \frac{1}{n} * \sum_{i=1}^{n}\left( \frac{x_1-\bar{X}}{S} \right)^4 = \frac{1}{n} * \sum_{i=1}^{n}z_i^4 \]
¿Cómo se ve la kurtosis?
En python podemos calcular la kurtosis con el método .kurt(). Ten en cuenta que este método resta 3 automáticamente, de manera que la comparación la hacemos con 0 o le podemos sumar 3 y comparar como habíamos especificado antes.
iris.kurt()## sepal_length -0.552064
## sepal_width 0.228249
## petal_length -1.402103
## petal_width -1.340604
## dtype: float64Conslusión
Conocer la asimetría de una variable nos hace conocer una característica más de la distribución. Una distribución muy asimétrica podría indicarnos mucha desigualdad, o también que nuestro esfuerzo podría enfocarte en pocos elementos con muy alto valor, y este tipo de decisiones son claves.
De cualquier modo, recuerda siempre acompañar cualquier estadístico con alguna representación gráfica pertinente para evitar malinterpretar los resultados.